题目内容
 嫦娥一号卫星的发射成功是中国深空探测迈出的第一步.为了给人类自己找到更大的生存空间和进一步的深空探测,目前人类已经有了在月球上建立永久研究基地的设想.假设在某次的登月探测研究中,宇航员在月球上以初速度v0向一个倾角为θ的斜坡水平抛出一个小球,测得经过时间t,小球垂直落在斜坡上的C点,如图所示.求:
嫦娥一号卫星的发射成功是中国深空探测迈出的第一步.为了给人类自己找到更大的生存空间和进一步的深空探测,目前人类已经有了在月球上建立永久研究基地的设想.假设在某次的登月探测研究中,宇航员在月球上以初速度v0向一个倾角为θ的斜坡水平抛出一个小球,测得经过时间t,小球垂直落在斜坡上的C点,如图所示.求:(1)小球落到斜坡上的速度大小v;
(2)月球表面附近的重力加速度g;
(3)设月球的半径为R,绕月球表面做匀速圆周运动的卫星的运行周期.
分析:(1)小球垂直落在斜坡上的C点时速度的方向与竖直方向之间的夹角是θ,利用速度的合成与分解可以求出小球落到斜坡上的速度大小v;
(2)根据运动学的公式求出月球表面附近的重力加速度g;
(3)月球表面的重力由万有引力提供,绕月球表面做匀速圆周运动的卫星的向心力与万有引力提供,写出公式即可求解.
(2)根据运动学的公式求出月球表面附近的重力加速度g;
(3)月球表面的重力由万有引力提供,绕月球表面做匀速圆周运动的卫星的向心力与万有引力提供,写出公式即可求解.
解答:解:(1)由速度的合成与分解图可知

sinθ=
所以:v=
(2)由图可知tanθ=
vy=gt
求出:g=
(3)设绕月卫星的周期为T,月球质量为M,卫星质量为m,
根据:
=mR
月球表面的重力由万有引力提供:
=mg
求得:T=
答:(1)小球落到斜坡上的速度大小v=
;
(2)月球表面附近的重力加速度g=
;
(3)设月球的半径为R,绕月球表面做匀速圆周运动的卫星的运行周期T=
.

sinθ=
| v0 |
| v |
所以:v=
| v0 |
| sinθ |
(2)由图可知tanθ=
| v0 |
| vy |
vy=gt
求出:g=
| v0 |
| t?tanθ |
(3)设绕月卫星的周期为T,月球质量为M,卫星质量为m,
根据:
| GMm |
| R2 |
| 4π2 |
| T2 |
月球表面的重力由万有引力提供:
| GMm |
| R2 |
求得:T=
|
答:(1)小球落到斜坡上的速度大小v=
| v0 |
| sinθ |
(2)月球表面附近的重力加速度g=
| v0 |
| t?tanθ |
(3)设月球的半径为R,绕月球表面做匀速圆周运动的卫星的运行周期T=
|
点评:该题把平抛运动与万有引力相结合,有一定的难度.根据相关的知识和公式即可求解.属于中档题目,

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目

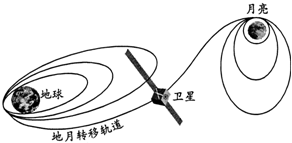 ks5如图是嫦娥一号卫星奔月的示意图,卫星发射后通过自带的小型火箭多次变轨,进入地月转移轨道,最终被月球引力捕获,成为绕月卫星,并开展对月球的探测,下列说法正确的是( )
ks5如图是嫦娥一号卫星奔月的示意图,卫星发射后通过自带的小型火箭多次变轨,进入地月转移轨道,最终被月球引力捕获,成为绕月卫星,并开展对月球的探测,下列说法正确的是( )