题目内容
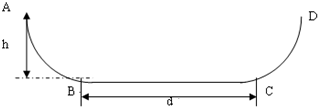
10. 如图所示,人用细绳通过光滑定滑轮拉起地面上的质量为m的物体A,A穿在光滑的竖直杆上沿杆以速度v匀速上升.某一时刻细绳与竖直杆的夹角为θ,则此时人拉细绳的速度为vcosθ,人拉力的功率为mgv.(重力加速度为g)
如图所示,人用细绳通过光滑定滑轮拉起地面上的质量为m的物体A,A穿在光滑的竖直杆上沿杆以速度v匀速上升.某一时刻细绳与竖直杆的夹角为θ,则此时人拉细绳的速度为vcosθ,人拉力的功率为mgv.(重力加速度为g)
分析 将A的速度分解为沿绳子方向和垂直于绳子方向,根据平行四边形定则求出A的实际运动的速度,再根据功能关系求出人做功的功率.
解答  解:将A的速度分解为沿绳子方向和垂直于绳子方向,如图所示,拉绳子的速度等于A沿绳子方向的分速度,
解:将A的速度分解为沿绳子方向和垂直于绳子方向,如图所示,拉绳子的速度等于A沿绳子方向的分速度,
根据平行四边形定则得,实际速度$v=\frac{{v}_{人}}{cosθ}$,人拉绳子的速度:v人=vcosθ;
在A匀速上升的过程中动能不变,重力势能增大,所以拉力的功率等于A克服重力做功的功率,即:P人=PA=mgv.
故答案为:vcosθ,mgv.
点评 解决本题的关键知道速度的合成与分解遵循平行四边形定则,注意会画出正确的速度的分解图.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
1.起重机把2.0×104 N的重物匀速提升10m,其输出功率是5.0×104 W.起重机( )
| A. | 用时4s | B. | 用时5s | C. | 做功8.0×105J | D. | 做功5.0×105J |
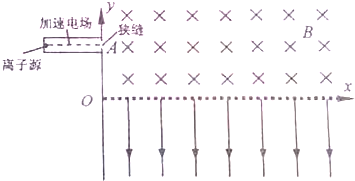
18. 如图所示,通电的圆线圈放置在水平面中固定不动,OO′是过圆心的竖直方向的轴线,从上向下看,线圈中的电流为逆时针方向.一个水平放置的较小的圆线圈从通电线圈的正上方由静止开始下落,途中先后经过位置Ⅰ、Ⅱ、Ⅲ时的加速度值分别为a1、a2、a3则( )
如图所示,通电的圆线圈放置在水平面中固定不动,OO′是过圆心的竖直方向的轴线,从上向下看,线圈中的电流为逆时针方向.一个水平放置的较小的圆线圈从通电线圈的正上方由静止开始下落,途中先后经过位置Ⅰ、Ⅱ、Ⅲ时的加速度值分别为a1、a2、a3则( )
 如图所示,通电的圆线圈放置在水平面中固定不动,OO′是过圆心的竖直方向的轴线,从上向下看,线圈中的电流为逆时针方向.一个水平放置的较小的圆线圈从通电线圈的正上方由静止开始下落,途中先后经过位置Ⅰ、Ⅱ、Ⅲ时的加速度值分别为a1、a2、a3则( )
如图所示,通电的圆线圈放置在水平面中固定不动,OO′是过圆心的竖直方向的轴线,从上向下看,线圈中的电流为逆时针方向.一个水平放置的较小的圆线圈从通电线圈的正上方由静止开始下落,途中先后经过位置Ⅰ、Ⅱ、Ⅲ时的加速度值分别为a1、a2、a3则( )| A. | a1=a2=a3=g | B. | a1<g,a2=g,a3<g | C. | a1<g,a2=0,a3>g | D. | a1<g,a2=0,a3<g |
5.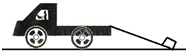 如图所示,运输人员要把质量为m的体积较小的木箱拉上汽车,现将长为L的木板搭在汽车的尾部与地面之间,构成一个固定的斜面,然后用平行斜面的力将木箱匀速拉上汽车,斜面与水平地面成30°角,木箱与斜面间的动摩擦因数为μ,重力加速度为g,则此过程拉力做功为( )
如图所示,运输人员要把质量为m的体积较小的木箱拉上汽车,现将长为L的木板搭在汽车的尾部与地面之间,构成一个固定的斜面,然后用平行斜面的力将木箱匀速拉上汽车,斜面与水平地面成30°角,木箱与斜面间的动摩擦因数为μ,重力加速度为g,则此过程拉力做功为( )
 如图所示,运输人员要把质量为m的体积较小的木箱拉上汽车,现将长为L的木板搭在汽车的尾部与地面之间,构成一个固定的斜面,然后用平行斜面的力将木箱匀速拉上汽车,斜面与水平地面成30°角,木箱与斜面间的动摩擦因数为μ,重力加速度为g,则此过程拉力做功为( )
如图所示,运输人员要把质量为m的体积较小的木箱拉上汽车,现将长为L的木板搭在汽车的尾部与地面之间,构成一个固定的斜面,然后用平行斜面的力将木箱匀速拉上汽车,斜面与水平地面成30°角,木箱与斜面间的动摩擦因数为μ,重力加速度为g,则此过程拉力做功为( )| A. | mg$\frac{L}{2}$ | B. | $\frac{1}{2}$mgL(1+2μ) | C. | $\frac{1}{2}$mgL(1+$\sqrt{3}$μ) | D. | $\frac{1}{2}$mgL(2+$\sqrt{3}$μ) |
15.一位质量为m的运动员从下蹲状态向上起跳,经△t时间,身体伸直并刚好离开地面,速度为v,在此过程中( )
| A. | 地面对他的冲量为mv+mg△t | B. | 地面对他的冲量为mv-mg△t | ||
| C. | 地面对他做的功为$\frac{1}{2}$mv2 | D. | 地面对他做的功为零 |
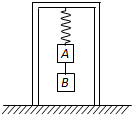 如图所示,在质量M=5kg的无下底的木箱顶部用一轻弹簧悬挂质量分别为ma=1kg、mb=0.5kg的A、B两物体,弹簧的劲度系数为100N/m.箱子放在水平地面上,平衡后剪断A、B间的连线,A将做简谐运动,求:(g=10m/s2)
如图所示,在质量M=5kg的无下底的木箱顶部用一轻弹簧悬挂质量分别为ma=1kg、mb=0.5kg的A、B两物体,弹簧的劲度系数为100N/m.箱子放在水平地面上,平衡后剪断A、B间的连线,A将做简谐运动,求:(g=10m/s2)