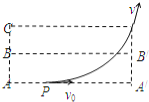��Ŀ����
����Ŀ����ͼ��ʾ��������Ϊm������B��C�ֱ������ʵ��ɵ�������˨�ӣ������Ƿ������Ϊ![]() �Ĺ⻬б���ϣ���ֹʱ���ɵ��α���Ϊ
�Ĺ⻬б���ϣ���ֹʱ���ɵ��α���Ϊ![]() ��б����й̶�����D������C���ڵ���D�ϣ�������ҲΪm������A��б���ϵ�ij���ɾ�ֹ�ͷţ�A��B��������֪�������ٶ�Ϊ
��б����й̶�����D������C���ڵ���D�ϣ�������ҲΪm������A��б���ϵ�ij���ɾ�ֹ�ͷţ�A��B��������֪�������ٶ�Ϊ![]() ������ʼ�մ��ڵ������ڣ����ƿ�����������
������ʼ�մ��ڵ������ڣ����ƿ�����������
��1�����ɵľ���ϵ��![]() ��
��
��2����A��B������ճ����һ��ʼ����г�˶�����A��B��һ���˶�����ߵ�ʱ��C�Ե���D��ѹ��ǡ��Ϊ�㣬��C�Ե���Dѹ�������ֵ��
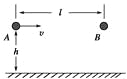
��3������A����һλ���ɾ�ֹ�ͷţ�A��B������ճ������������һ���˶����ҵ�B��һ���˶�����ߵ�ʱ��C�Ե���D��ѹ��Ҳǡ��Ϊ�㣮��֪A��B�����ɵ�һ�λָ�ԭ��ʱB���ٶȴ�СΪ![]() ����������A��һ���˶��ﵽ����ߵ��뿪ʼ��ֹ�ͷŵ�֮��ľ��룮
����������A��һ���˶��ﵽ����ߵ��뿪ʼ��ֹ�ͷŵ�֮��ľ��룮

���𰸡���1��![]() ,��2��3mg,��3��
,��2��3mg,��3��![]() .
.
�������������������1����B����������������ƽ������������ɵľ���ϵ������2�����ݼ�г�˶��ص�����ظ�����Ȼ��Ӧ��ƽ��������ţ�ٵ����������C��D�����ѹ������3����AӦ�û�е���غ㶨�����A��B��ײǰA���ٶȣ��ɶ����غ㶨�������ײ��A��B���ٶȣ���A��B��ɵ�ϵͳ��B��C��ɵ�ϵͳ����A����BӦ�û�е���غ㶨�ɣ��������⣮
��1������B��ֹʱ�������α���Ϊx0�����ɵĵ���![]() ������B������ͼ��ʾ
������B������ͼ��ʾ
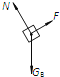
��ƽ�������ã� ![]()
��ã����ɵľ���ϵ��![]()
��2��A��B����һ������г�˶�����ߵ�ʱ������C�Ե���D��ѹ����СΪ0
���C�����ɵ����� ![]()
��A��B���ظ������ ![]()
�ɼ�г�˶��ĶԳ��ԣ���֪A��B����һ������г�˶�����͵�ʱ���ظ���Ҳ���
��![]() ����ʱ����C�Ե���D��ѹ�����
����ʱ����C�Ե���D��ѹ�����
������A��B�� ![]()
�ɵ����� ![]()
������C���赲��D������C�ĵ���ΪN
�� ![]()
��ţ�ٵ������ɿ�֪������C�Ե���D��ѹ����С�� ![]()
����C�Ե���Dѹ�������ֵΪ![]()
��3��������A�ͷ�ʱA��B֮�����Ϊx��A��B����ǰ����A�ٶȵĴ�СΪ![]()
������A���ӿ�ʼ�»���A��B����ǰ�Ĺ������ɻ�е���غ㶨�ɵã� ![]()
��ã� ![]() ��
��
��A��B�����������干ͬ�ٶȵĴ�СΪ![]() ��A��B������ײ�Ĺ��̶����غ�
��A��B������ײ�Ĺ��̶����غ�
����ǰA���ٶȷ���Ϊ�������ɶ����غ㶨�ɵã� ![]()
��ã� ![]() ��
��
����B��ֹʱ���ɵ��α���Ϊ![]() ���赯������Ϊ
���赯������Ϊ![]() ����A��B��ʼѹ�����ɵ����ɵ�һ�λָ�ԭ���Ĺ���
����A��B��ʼѹ�����ɵ����ɵ�һ�λָ�ԭ���Ĺ���
�ɻ�е���غ㶨�ɵã� ![]() ��
��
�����ɵ�һ�λָ�ԭ��ʱA��Bǡ�÷��룬����������A������б�������ľ���Ϊ![]()
������A������B���뵽��ߵ�Ĺ��̣���е���غ����ɻ�е���غ㶨�ɵã� ![]()
��ã� ![]()
������B��C�͵�������ɵ�ϵͳ������B�˶�����ߵ�ʱ�ٶ�Ϊ0
����Cǡ���뿪����D����ʱ���ɵ��쳤��ҲΪ![]() �����ɵĵ�������ҲΪ
�����ɵĵ�������ҲΪ![]()
��A��B���뵽B�˶�����ߵ�Ĺ������ɻ�е���غ㶨�ɵã� ![]()
��ã� ![]() ��
��
�ɢ٢ڢۢܽ�ã� ![]()
�ɼ��ι�ϵ�ɵã�����A��һ���˶��ﵽ����ߵ��뿪ʼ��ֹ�ͷŵ�֮��ľ��룺 ![]()

 ��������ϵ�д�
��������ϵ�д� ���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д�