题目内容
6．
如图所示，在一个直立的光滑管内放置一个轻质弹簧，上端O点与管口A的距离为2x0，一个质量为m的小球从管口由静止下落，将弹簧压缩至最低点B，压缩量为x0，不计空气阻力，在向下运动中下列说法正确的是（ ）| A． | 小球运动的最大速度等于2$\sqrt{g{x}_{0}}$ | |
| B． | 弹簧的劲度系数为$\frac{mg}{{x}_{0}}$ | |
| C． | 小球接触弹簧后的运动过程中重力势能与弹性势能之和先减小后增大 | |
| D． | 弹簧的最大弹性势能为3mgx0 |
分析 根据机械能守恒定律求出小球运动到O点的速度，再分析小球接触弹簧后的运动情况．借助简谐运动的模型分析小球的最大加速度．根据机械能守恒求解弹簧的最大弹性势能．
解答 解：A、设小球刚运动到O点时的速度为v，则有mg•2x0=$\frac{1}{2}m{v}^{2}$，v=2$\sqrt{g{x}_{0}}$．小球接触弹簧后先做加速运动，所以小球运动的最大速度大于2$\sqrt{g{x}_{0}}$．故A错误；
B、设弹簧的弹力与重力大小相等时，弹簧压缩量为x，则有mg=kx，k=$\frac{mg}{x}$．而弹簧的弹力与重力平衡的位置在B点的上方，则x＜x0，则k＞$\frac{mg}{{x}_{0}}$．故B错误；
C、小球刚接触弹簧后先做加速运动再做减速运动，根据系统机械能守恒可知小球的重力势能、弹簧的弹性势能和小球的动能之和保持不变，因小球动能先增加后减小，故重力势能与弹性势能之和先减小后增加，故C正确；
D、当小球运动到最低点B时，弹性势能最大，根据机械能守恒定律得，弹簧的最大弹性势能为3mgx0．故D正确．
故选：CD．
点评 本题既要根据受力情况判断小球的运动情况，又要运用机械能守恒分析小球的速度和弹性势能，综合性较强．
练习册系列答案
相关题目
19．关于做平抛运动的物体，下列说法中正确的是（ ）
| A． | 加速度越来越大 | |
| B． | 在相同时间内速度的增量越来越大 | |
| C． | 速度方向与加速度方向的夹角越来越大 | |
| D． | 重力的功率越来越大 |
20．一质量为m的物体静止在粗糙水平地面上，现用一大小为F的水平拉力拉动物体，经过一段时间后其速度变为v，重力加速度为g，则（ ）
| A． | 在这段时间内，摩擦力做的功为零 | |
| B． | 在这段时间内，拉里做的功为$\frac{1}{2}$mv2 | |
| C． | 物体的速度为v时，拉力的功率为Fv | |
| D． | 物体的速度为v时，重力的功率为mgv |
如图在一矩形区域内，不加磁场时，不计重力的带电粒子以某一初速度垂直左边界射入，穿过区域的时间为t0，若加上磁感应强度为B，水平向里的匀强磁场，带电粒子仍以原来的初速度入射，粒子飞出偏离原方向30°．求：
1．
如图所示，小球自a点由静止自由下落，到b点时与竖直弹簧接触，d点是小球运动的最低点，bc=cd．不计弹簧质量和空气阻力，小球在由a到d向下运动过程中，下列说法正确的是（ ）
如图所示，小球自a点由静止自由下落，到b点时与竖直弹簧接触，d点是小球运动的最低点，bc=cd．不计弹簧质量和空气阻力，小球在由a到d向下运动过程中，下列说法正确的是（ ）| A． | 小球的机械能守恒 | |
| B． | 小球在b点时其重力做功功率最大 | |
| C． | 到c点时小球的动能最大 | |
| D． | 由a到d的整个过程中小球重力势能的减小量等于弹簧弹性势能的增加量 |
11．下列说法中正确的是（ ）
| A． | 伽利略猜想自由落体的运动速度与下落时间成正比，并直接用实验进行了验证 | |
| B． | 牛顿第一定律、牛顿第二定律都可以通实验来验证 | |
| C． | 单位m、kg、s是一组属于国际单位制的基本单位 | |
| D． | 用比值法定义的物理概念在物理学中占有相当的比例，例如加速度a=$\frac{F}{m}$就是采用比值定义法 |
18．
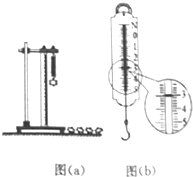某同学利用如图（a）所示的装置做“探究弹簧测力计大小与其长度的关系”的实验．
（1）在安装刻度尺时，必须使刻度尺保持竖直状态．
（2）下表是他实验测得的该弹簧测力计大小F与弹簧长度x的关系的几组数据：
由表中数据可得，该弹簧的原长x0=4.0cm，劲度系数k=50N/m．
（3）他又利用实验原理把该弹簧做成一把弹簧秤，当弹簧秤上的示数如图（b）示数时，该弹簧的长度x=10.0cm．
某同学利用如图（a）所示的装置做“探究弹簧测力计大小与其长度的关系”的实验．（1）在安装刻度尺时，必须使刻度尺保持竖直状态．
（2）下表是他实验测得的该弹簧测力计大小F与弹簧长度x的关系的几组数据：
| 弹簧弹力F/N | 0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| 弹簧的长度x/cm | 4.0 | 6.0 | 8.0 | 10.0 | 12.0 | 14.0 | 16.0 |
（3）他又利用实验原理把该弹簧做成一把弹簧秤，当弹簧秤上的示数如图（b）示数时，该弹簧的长度x=10.0cm．
15．
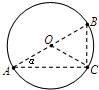如图所示，在匀强电场中有一半径为R的圆，场强方向与圆所在平面平行，场强大小为Ep，有一电荷量为q的带正电微粒以相同的初动能沿着各个方向从A点进入圆形区域中，只在电场力作用下运动，从圆周上不同点离开圆形区域，其中从C点离开圆形区域的带电微粒的动能最大，图中O是圆心，AB是圆的直径，AC是与AB成α角的弦，则（ ）
如图所示，在匀强电场中有一半径为R的圆，场强方向与圆所在平面平行，场强大小为Ep，有一电荷量为q的带正电微粒以相同的初动能沿着各个方向从A点进入圆形区域中，只在电场力作用下运动，从圆周上不同点离开圆形区域，其中从C点离开圆形区域的带电微粒的动能最大，图中O是圆心，AB是圆的直径，AC是与AB成α角的弦，则（ ）| A． | 匀强电场的方向沿CO方向 | |
| B． | A、C两点之间的电势差为2ERcos2α | |
| C． | 该带电微粒在C带电电势能大于在A点的电势能 | |
| D． | 从A到C电场力做功为2qERcosα |
16．2014年10月24日2点00分，我国自行研制的探月工程三期返回飞行试验器，在西昌卫星发射中心用长征三号丙运载火箭发射升空．若返回飞行试验器变轨后沿圆形轨道环绕月球运行，运行周期为T．已知月球半径为R，月球表面的重力加速度为g．则飞船离月球表面的高度为（ ）
| A． | $\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}$-R | B． | $\root{3}{\frac{gR{T}^{2}}{4{π}^{2}}}$-R | C． | $\root{3}{\frac{G{R}^{2}{T}^{2}}{4{π}^{2}}}$-R | D． | $\root{3}{\frac{g{R}^{2}T}{4{π}^{2}}}$-R |