题目内容
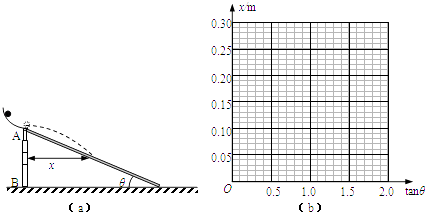
【题目】用图甲所示装置“探究加速度与力、质量的关系”.请思考并完成相关内容: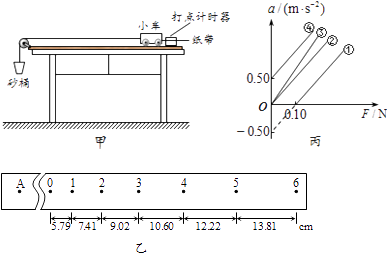
(1)实验时,为平衡摩擦力,以下操作正确的是
A.连着砂桶,适当调整木板右端的高度,直到小车被轻推后沿木板匀速运动
B.取下砂桶,适当调整木板右端的高度,直到小车被轻推后沿木板匀速运动
C.取下砂桶,适当调整木板右端的高度,直到小车缓慢沿木板做直线运动
(2)图乙是实验中得到的一条纸带,已知相邻计数点间还有四个点未画出,打点计时器所用电源频率为50Hz,由此可求出小车的加速度a=m/s2(计算结果保留三位有效数字).
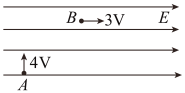
(3)一组同学在保持木板水平时,研究小车质量一定的情况下加速度a与合外力F的关系,得到如图丙中①所示的a﹣F图线.则小车运动时受到的摩擦力f=N;小车质量M=kg.若该小组正确完成了步骤(1),得到的a﹣F图线应该是图丙中的(填“②”、“③”或“④”).
【答案】
(1)B
(2)1.60
(3)0.10;0.20;②
【解析】解:(1)平衡摩擦力时,取下砂桶,适当当调整木板右端的高度,直到小车被轻推后沿木板匀速运动,故B正确.(2)根据△x=aT2 , 运用逐差法得,a= ![]() =
= ![]() =1.60m/s2 . (3)根据图①知,当F=0.10N时,小车才开始运动,可知小车运动时受到的摩擦力f=0.10N,图线的斜率表示质量的倒数,则m=
=1.60m/s2 . (3)根据图①知,当F=0.10N时,小车才开始运动,可知小车运动时受到的摩擦力f=0.10N,图线的斜率表示质量的倒数,则m= ![]() kg=0.20kg.
kg=0.20kg.
平衡摩擦力后,a与F成正比,图线的斜率不变,故正确图线为②.
故答案为:(1)B;(2)1.60;(3)0.10,0.20,②.
(1)平衡摩擦力时应取下砂桶,调整木板右端高度,轻推小车,小车能够沿木板做匀速直线运动即可.(2)根据连续相等时间内的位移之差是一恒量,运用逐差法求出小车的加速度.(3)根据图线的横轴截距求出小车运动时受到的摩擦力大小,结合图线的斜率求出小车质量.平衡摩擦力后,抓住图线斜率不变,a与F成正比确定正确的图线.

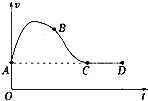
【题目】如图所示,AB是一可升降的竖直支架,支架顶端A处固定一弧形轨道,轨道末端水平.一条形木板的上端铰接于过A的水平转轴上,下端搁在水平地面上.将一小球从弧型轨道某一位置由静止释放,小球落在木板上的某处,测出小球平抛运动的水平射程x和此时木板与水平面的夹角θ,并算出tanθ.改变支架AB的高度,将小球从同一位置释放,重复实验,得到多组x和tanθ,记录的数据如表:
实验次数 | 1 | 2 | 3 | 4 | 5 | 6 |
tanθ | 0.18 | 0.32 | 0.69 | 1.00 | 1.19 | 1.43 |
x/m | 0.035 | 0.065 | 0.140 | 0.160 | 0.240 | 0.290 |
(1)在图(b)的坐标中描点连线,做出x﹣tanθ的关系图象;
(2)根据x﹣tanθ图象可知小球做平抛运动的初速度v0=m/s;实验中发现θ超过60°后,小球将不会掉落在斜面上,则斜面的长度为 m.(重力加速度g取10m/s2);
(3)实验中有一组数据出现明显错误,可能的原因是 .