题目内容
5. 如图所示,重为G的物体在与水平方向成θ角的拉力F作用下沿水平面做匀速运动,已知物体与地面间的动摩擦因数μ=$\frac{\sqrt{3}}{3}$,θ=45°.求:
如图所示,重为G的物体在与水平方向成θ角的拉力F作用下沿水平面做匀速运动,已知物体与地面间的动摩擦因数μ=$\frac{\sqrt{3}}{3}$,θ=45°.求:(1)拉力F的大小;
(2)拉力与水平方向的夹角θ多大时拉力最小?
分析 (1)对物体受力分析,然后根据平衡条件并结合正交分解法列式求解;
(2)受力分析后根据平衡条件并结合正交分解法推导出拉力的表达式进行分析,得到最小值.
解答 解:(1)对物体受力分析,如图所示:
根据平衡条件,有:
水平方向:Fcos45°-f=0
竖直方向:N+Fsin°-mg=0
其中:f=μN
联立解得:F=$\frac{μmg}{cos45°+μsin45°}$=$\frac{\frac{\sqrt{3}}{3}×G}{\frac{\sqrt{2}}{2}+\frac{\sqrt{3}}{3}×\frac{\sqrt{2}}{2}}$=$\frac{\sqrt{2}}{\sqrt{3}+1}G≈0.52G$
(2)对物体受力分析,根据平衡条件,有:
水平方向:Fcosθ-f=0
竖直方向:N+Fsinθ-mg=0
其中:f=μN
联立解得:F=$\frac{μmg}{cosθ+μsinθ}$=$\frac{\frac{\sqrt{3}}{3}G}{cosθ+\frac{\sqrt{3}}{3}sinθ}$=$\frac{\frac{\sqrt{3}}{3}G}{\frac{2}{3}\sqrt{3}(\frac{\sqrt{3}}{2}cosθ+\frac{1}{2}sinθ)}$=$\frac{\frac{\sqrt{3}}{3}G}{\frac{2\sqrt{3}}{3}sin(θ+30°)}$=$\frac{G}{2sin(θ+30°)}$
当θ=60°时,拉力最小,为$\frac{G}{2}$;
答:(1)拉力F的大小为0.52G;
(2)拉力与水平方向的夹角θ为60°时,拉力最小,为$\frac{G}{2}$.
点评 本题关键是根据平衡条件并采用正交分解法列式后列式并解方程组,第二问是动态分析问题,要用三角函数求解极值,较难.

 如图所示,在匀强磁场中固定放置一根串接一电阻R的直角形金属导轨aOb(在纸面内),磁场方向垂直于纸面朝里,另有两根金属导轨c、d分别平行于Oa、Ob放置.保持导轨之间接触良好,金属导轨的电阻不计.现经历以下四个过程:
如图所示,在匀强磁场中固定放置一根串接一电阻R的直角形金属导轨aOb(在纸面内),磁场方向垂直于纸面朝里,另有两根金属导轨c、d分别平行于Oa、Ob放置.保持导轨之间接触良好,金属导轨的电阻不计.现经历以下四个过程:①以速率v移动d,使它与Ob的距离增大一倍;
②再以速率v移动c,使它与Oa的距离减小一半;
③然后,再以速率2v移动c,使它回到原处;
④最后以速率2v移动d,使它也回到原处.
设上述四个过程中通过电阻R的电量大小依次为Q1、Q2、Q3和Q4,则( )
| A. | Q1=Q2=Q3=Q4 | B. | Q1=Q2=2Q3=2Q4 | C. | 2Q1=2Q2=Q3=Q4 | D. | Q1≠Q2=Q3≠Q4 |
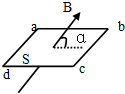 如图所示,矩形导体线框abcd放置在水平面内.磁场方向与水平方向成α角,已知cosα=$\frac{3}{5}$,回路面积为S,磁感应强度为B,则通过线框的磁通量为( )
如图所示,矩形导体线框abcd放置在水平面内.磁场方向与水平方向成α角,已知cosα=$\frac{3}{5}$,回路面积为S,磁感应强度为B,则通过线框的磁通量为( )| A. | BS | B. | $\frac{4}{5}$BS | C. | $\frac{3}{5}$BS | D. | $\frac{3}{4}$BS |

| A. | 氢原子跃迁时放出的光子的能量是连续的 | |
| B. | 电子的轨道半径越小,氢原子能量越小 | |
| C. | 处于基态的氢原子是最稳定的 | |
| D. | 欲使处于基态的氢原子激发,可用11eV的光子照射 |
| A. | 汽车匀速上坡 | |
| B. | 汽车在上坡过程中机械能减小 | |
| C. | 汽车在上坡过程中机械能增大 | |
| D. | 汽车在上坡过程中,动能减小,势能增大,总的机械能不变 |
 如图,质量为m的质点在三个共点恒力F1、F2和F3的作用下沿水平直线OO′匀速运动,下列说法正确的是( )
如图,质量为m的质点在三个共点恒力F1、F2和F3的作用下沿水平直线OO′匀速运动,下列说法正确的是( )| A. | 质点受到的合力不为零 | |
| B. | 质点受到的合力不为零,方向沿直线OO′ | |
| C. | 力F2和F3的合力方向与F1方向相同 | |
| D. | 撤去F1后,质点的加速度大小为$\frac{{F}_{1}}{m}$ |
 长为L的细线,拴一个质量为m的小球,一端固定于O点,让其在水平面内做匀速圆周运动(这种运动通常称为圆锥摆运动),如图所示,当摆线与竖直 方向的夹角为θ时,求:
长为L的细线,拴一个质量为m的小球,一端固定于O点,让其在水平面内做匀速圆周运动(这种运动通常称为圆锥摆运动),如图所示,当摆线与竖直 方向的夹角为θ时,求: 为了研究过山车的原理,物理小组提出了下列的设想:取一个与水平方向夹角为37°、长为L=2.0m的粗糙的倾斜轨道AB,通过水平轨道BC与竖直圆轨道相连,出口为水平轨道DE,整个轨道除AB段以外都是光滑的.其中AB与BC轨道以微小圆弧相接,如图所示.一个小物块以初速度v0=4.0m/s,从某一高处水平抛出,到A点时速度方向恰沿AB方向,并沿倾斜轨道滑下.已知物块与倾斜轨道的动摩擦因数μ=0.5(g取10m/s2,sin37°=0.6,cos37°=0.8)求:
为了研究过山车的原理,物理小组提出了下列的设想:取一个与水平方向夹角为37°、长为L=2.0m的粗糙的倾斜轨道AB,通过水平轨道BC与竖直圆轨道相连,出口为水平轨道DE,整个轨道除AB段以外都是光滑的.其中AB与BC轨道以微小圆弧相接,如图所示.一个小物块以初速度v0=4.0m/s,从某一高处水平抛出,到A点时速度方向恰沿AB方向,并沿倾斜轨道滑下.已知物块与倾斜轨道的动摩擦因数μ=0.5(g取10m/s2,sin37°=0.6,cos37°=0.8)求: