��Ŀ����
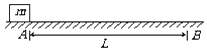
����Ŀ����ͼ��ʾ������Ϊ2kg���ϱ���⻬��ľ���ֹ�ڹ⻬ˮƽ���ϣ�����Ϊ1kg����Ϊ�ʵ��С���������ľ����Ҷˣ�����Ϊ4kg��ľ������5m/s���ٶ������˶�����ľ�����ײ�Ժ�С���廬��ľ�����ϣ�ľ����8m/s���ٶȣ�ľ�����ϱ�����С����Ķ�Ħ������Ϊ0.2����g=10m/s2���� 
��1��С������ľ�����ϱ��滬�жʱ�����ľ���Ҿ�ֹ��
��2��ҪʹС���岻��ľ�����ϻ��䣬ľ��������Ҫ���
���𰸡�
��1���⣺�������ײ������ϵͳ�Ķ����غ㣬���ҵij��ٶȷ���Ϊ�������ɶ����غ㶨�ɵ�
m��v��=m��v����+m��v����
��� v����=1m/s
С���������ϻ������й�ͬ�ٶ�v����С���������ɵ�ϵͳ���ɶ����غ㶨�ɵ�
m��v����=��m��+m����v
��С���壬�ɶ��������� ��mgt=m��v��0��
������� t=0.4s
��С������ľ�����ϱ��滬��0.4sʱ�����ľ���Ҿ�ֹ��
��2���⣺��С�������վ���ľ������˵�������Ϊx����
x= ![]() t��
t�� ![]() =
= ![]() t=
t= ![]() ��0.4m=0.2m
��0.4m=0.2m
����ľ���ҵij�������ҪΪ0.2m��
��ҪʹС���岻��ľ�����ϻ��䣬ľ��������Ҫ0.2m��
����������1��������ײ�Ĺ��������㶯���غ㣬���ݶ����غ������������ٶȣ��ٸ��ݶ���������ʽ���ʱ�䡣
��2��С���岻��ľ���ϻ��䣬������֮��λ��֮��Ӧ��С��ľ��ij��ȡ�
�����㾫����������Ҫ�����˶����غ㶨�ɵ����֪ʶ�㣬��Ҫ���ն����غ㶨�ɳ�����������ϵͳ����������ϵͳ���������ĺ���Ϊ�㣻ϵͳ���ܵ������ĺ����䲻Ϊ�㣬��ϵͳ����������С�öࣻϵͳ���������ĺ����䲻Ϊ�㣬����ij�������ϵķ���Ϊ�㣬���ڸ÷�����ϵͳ���ܶ����ķ������ֲ��������ȷ�����⣮