Question

如图（a）所示，A、B为水平放置的平行金属板，板间距离为d（d远小于板的长和宽）．在两板之间有一带负电的质点P．已知若在A、B间加电压U_o，则质点P可以静止平衡．现在A、B间加上如图（b）所示的随时间t变化的电压u．在t=0时质点P位于A、B间的中点处且初速为零．已知质点P能在A、B之间以最大的幅度上下运动而又不与两板相碰，求图（b）中u改变的各时刻t₁、t₂、t₃及t_n的表达式．（质点开始从中点上升到最高点，及以后每次从最高点到最低点或从最低点到最高点的过程中，电压只改变一次．）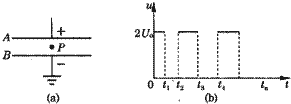

Answer 1

设质点P的质量为m，电量大小为q，根据题意，当A、B间的电压为U₀时，有
?

qU0

d

=mg，
?当两板间的电压为2U₀时，P的加速度向上，其大小为a，则

2qU0

d

-mg=ma，
?解得a=g．
?当两板间的电压为零时，P自由下落，加速度为g，方向向下．
?在t=0时，两板间的电压为2U₀，P自A、B间的中点向上做初速度为零的匀加速运动，加速度为g．设经过时间τ₁，P的速度变为v₁，此时使电压变为零，让P在重力作用下做匀减速运动，再经过时间τ₁′，P正好到达A板且速度为零，故有
?v₁=gτ₁，0=v₁-gτ₁′，
?

1

2

d=

1

2

gτ₁²+v₁τ₁′-

1

2

gτ₁′²，
?由以上各式，得
?τ₁=τ₁′，τ₁=

2

2

d g

，
?因为t₁=τ₁，得t₁=

2

2

d g

．
?在重力作用下，P由A板处向下做匀加速运动，经过时间τ₂，速度变为v₂，方向向下，这时加上电压使P做匀减速运动，经过时间τ₂′，P到达B板且速度为零，故有
?v₂=gτ₂，0=v₂-gτ₂′，
?d=

1

2

gτ₂²+v₂τ₂′-

1

2

gτ₂′²，
?由以上各式，得τ₂=τ₂′，τ₂=

d g

，
?因为t₂=t₁+τ₁′+τ₂，
?得t₂=（

2

+1）

d g

．
?在电场力与重力的合力作用下，P由B板处向上做匀加速运动，经过时间τ₃，速度变为v₃，此时使电压变为零，让P在重力作用下做匀减速运动．经过时间τ₃′，P正好到达A板且速度为零，故有
?v₃=gτ₃，0=v₃-gτ₃′，
?d=

1

2

gτ₃²+v₃τ₃′-

1

2

gτ₃′²
?由上得τ₃=τ₃′，τ₃=

d g

，
?因为t₃=t₂+τ₂′+τ₃，
?得t₃=（

2

+3）

d g

．
?根据上面分析，因重力作用，P由A板向下做匀加速运动，经过时间τ₂，再加上电压，经过时间τ₂′，P到达B且速度为零，因为t₄=t₃+τ₃′+τ₂，
?得t₄=（

2

+5）

d g

．
?同样分析可得
?t_n=（

2

+2n-3）

d g

．（n≥2）
故图（b）中u改变的各时刻t₁=

2

2

d g

，t₂=（

2

+1）

d g

，t₃=（

2

+3）

d g

，及t_n=（

2

+2n-3）

d g

（n≥2）．