题目内容
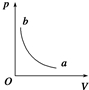
17. 如图所示,在同一竖直平面内有两个正对着的半圆形光滑绝缘轨道,轨道的半径都是R.轨道端点所在的水平线相隔一定的距离x.一质量为m,带正电q的小球能在其间运动而不脱离轨道,经过最低点B时的速度为v.小球在最低点B与最高点A对轨道的压力之差为为△F(△F>0).若当小球运动到最低点B时,加一方向竖直向上的匀强电场E(E<$\frac{mg}{q}$),则小球在最低点B与最高点A对轨道的压力之差为为△F′(△F′>0).不计空气阻力.则( )
如图所示,在同一竖直平面内有两个正对着的半圆形光滑绝缘轨道,轨道的半径都是R.轨道端点所在的水平线相隔一定的距离x.一质量为m,带正电q的小球能在其间运动而不脱离轨道,经过最低点B时的速度为v.小球在最低点B与最高点A对轨道的压力之差为为△F(△F>0).若当小球运动到最低点B时,加一方向竖直向上的匀强电场E(E<$\frac{mg}{q}$),则小球在最低点B与最高点A对轨道的压力之差为为△F′(△F′>0).不计空气阻力.则( )| A. | m、R一定时,v变大,△F一定变大 | |
| B. | m、R一定时,x变大,△F一定变大 | |
| C. | 其他条件不变时,加电场前后,△F=△F′ | |
| D. | 其他条件不变时,加电场前后,△F>△F′ |
分析 由动能定理求出A、B两点间的速度关系,由牛顿第二定律求出在A、B两点支持力,求出A、B两点支持力之差,然后分析答题.
解答 解:A、设m在A点时的速度为VA,在B点时速度为VB,对m从A到B点时,根据动能定理有:
mg(2R+X)=$\frac{1}{2}$mVB2-$\frac{1}{2}$mVA2
对m在B点时,受重力和支持力NB的作用,根据牛顿第二定律:
NB-mg=m$\frac{{v}_{B}^{2}}{R}$,所以:NB=mg+m$\frac{{v}_{B}^{2}}{R}$;
对m在A点,受重力和支持力NA,根据牛顿第二定律:
NA+mg=m$\frac{{v}_{A}^{2}}{R}$,所以:NA=m$\frac{{v}_{A}^{2}}{R}$-mg;
小球在最低点B与最高点A对轨道的压力之差△F=NB-NA=6mg+2mg$\frac{x}{R}$,
从推导的关系式可知,m、R一定时,当x变大时,从关系式中不难发现△F一定越大,故A错误,B正确.
C、加上电场后,从A到B过程,由动能定理得:(mg-qE)(2R+x)=$\frac{1}{2}$mvB′2-$\frac{1}{2}$mvA′2
对m在B点时,受重力和支持力NB′的作用,根据牛顿第二定律:
NB′-mg+qE=m$\frac{v{′}_{B}^{2}}{R}$,所以:NB′=mg+m$\frac{v{′}_{B}^{2}}{R}$-qE,
对m在A点,受重力和支持力NA′,根据牛顿第二定律:
NA′+mg-qE=m$\frac{v{′}_{A}^{2}}{R}$,所以:NA′=m$\frac{v{′}_{A}^{2}}{R}$-mg+qE;
小球在最低点B与最高点A对轨道的压力之差△F′=NB′-NA′=6(mg-qE)+2(mg-qE)$\frac{x}{R}$,
△F-△F′=6qE+2qE$\frac{x}{R}$>0,则:△F>△F′,故C错误,D正确;
故选:BD.
点评 把动能定理和圆周运动的知识结合在一起,这也是学习过程中常见的题目类型,只要掌握住分析问题的方法,这一类的题目基本上就可以解决了.

| A. | 电磁波传播不需要依赖介质 | |
| B. | γ射线比伦琴射线频率更高,穿透能力更强 | |
| C. | 红外线的显著作用是化学作用 | |
| D. | 狭义相对论基本假设的是在不同的惯性系中时间间隔具有相对性 | |
| E. | 把一个静止质量为m0的粒子,加速到0.6c(c为真空中的光速),需做的功为0.25m0c2 |
 如图所示,某同学用硬塑料管和一个质量为m的铁质螺丝帽研究匀速圆周运动,将螺丝帽套在塑料管上,手握塑料管使其保持竖直并在水平方向做半径为r的匀速圆周运动,则只要运动角速度合适,螺丝帽恰好不下滑,假设螺丝帽与塑料管间的动摩擦因数为μ,认为最大静摩擦力近似等于滑动摩擦力.则在该同学手转塑料管使螺丝帽恰好不下滑时,下述分析正确的是( )
如图所示,某同学用硬塑料管和一个质量为m的铁质螺丝帽研究匀速圆周运动,将螺丝帽套在塑料管上,手握塑料管使其保持竖直并在水平方向做半径为r的匀速圆周运动,则只要运动角速度合适,螺丝帽恰好不下滑,假设螺丝帽与塑料管间的动摩擦因数为μ,认为最大静摩擦力近似等于滑动摩擦力.则在该同学手转塑料管使螺丝帽恰好不下滑时,下述分析正确的是( )| A. | 螺丝帽受的重力与最大静摩擦力平衡 | |
| B. | 螺丝帽受到杆的弹力方向水平向外,背离圆心 | |
| C. | 此时手转动塑料管的角速度ω=$\sqrt{\frac{mg}{μr}}$ | |
| D. | 若杆的转动加快,螺丝帽有可能相对杆发生运动 |
| A. | 刮胡须的刀片的影子边缘模糊不清是光的衍射现象 | |
| B. | 红外线是波长比可见光波长更短的电磁波,常用于医院杀菌和消毒 | |
| C. | 电磁波和声波由空气进入水中,波长均变小 | |
| D. | 火车若接近光速行驶,我们在地面上看到车厢前后距离变大而车厢的高度不变 |
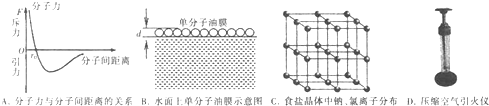
| A. | 分子间距离为r0时,分子间不存在引力和斥力 | |
| B. | 估测油酸分子直径大小d 时,不可把油酸分子简化为球形处理 | |
| C. | 猛推活塞,密闭的气体温度升高,压强变大,气体对外界做正功 | |
| D. | 食盐晶体中的钠、氯离子按一定规律分布,具有空间上的周期性 |
| A. | 质量小于120kg | B. | 质量等于120kg | ||
| C. | 质量大于120kg | D. | 由于失重,质量为零 |