题目内容
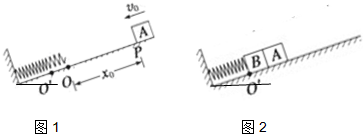 如图1所示,轻弹簧一端固定在与斜面垂直的挡板上,另一端点在O位置.质量为m的物块A(可视为质点)以初速度v0从距O点为x0的P点沿斜面向下运动,与弹簧接触后压缩弹簧,将弹簧右端压到O′点位置后,A又被弹簧弹回.A离开弹簧后,恰好回到P点.物块A与斜面间的动摩擦因数为μ,斜面倾角为37°.求:
如图1所示,轻弹簧一端固定在与斜面垂直的挡板上,另一端点在O位置.质量为m的物块A(可视为质点)以初速度v0从距O点为x0的P点沿斜面向下运动,与弹簧接触后压缩弹簧,将弹簧右端压到O′点位置后,A又被弹簧弹回.A离开弹簧后,恰好回到P点.物块A与斜面间的动摩擦因数为μ,斜面倾角为37°.求:(1)O点和O′点间的距离x1.
(2)如图2若将另一个与A完全相同的物块B(可视为质点)与弹簧右端拴接,将A与B并排在一起,使弹簧仍压缩到O′点位置,然后从静止释放,A、B共同滑行一段距离后分离.分离后物块A沿斜面向上滑行的最大距离x2是多少?
分析:(1)对全过程分析,抓住末动能为零,弹力做功为零,只有摩擦力做功,结合动能定理求出O点和O′点间的距离x1.
(2)根据动能定理,对O′到P过程分析,求出弹簧做功的大小,A、B将在弹簧原长处分离,对AB系统研究,运用动能定理求出分离时的动能,再分离对A分析,运用动能定理求出上滑的最大距离.
(2)根据动能定理,对O′到P过程分析,求出弹簧做功的大小,A、B将在弹簧原长处分离,对AB系统研究,运用动能定理求出分离时的动能,再分离对A分析,运用动能定理求出上滑的最大距离.
解答:解:(1)A从向下运动到再次返回到P的过程,根据动能定理有:
2μmg(x0+x1)=
mv02
解得:x1=
-x0
(2)A从O′到P过程设弹簧弹力做功为W,根据动能定理有:
W-μmg(x0+x1)cosθ-mgsinθ(x0+x1)=0
A、B将在弹簧原长处分离,设此时共同速度为v,根据动能定理有:W-2μmgx1cosθ-2mgx1sinθ=
2mv12
分离后对A有:μmgx2cosθ+mgx2sinθ=
mv12
联立以上各式可得:x2=x0-
.
答:(1)O点和O′点间的距离x1=
-x0.
(2)分离后物块A沿斜面向上滑行的最大距离x2是x2=x0-
.
2μmg(x0+x1)=
| 1 |
| 2 |
解得:x1=
| 5v02 |
| 16μg |
(2)A从O′到P过程设弹簧弹力做功为W,根据动能定理有:
W-μmg(x0+x1)cosθ-mgsinθ(x0+x1)=0
A、B将在弹簧原长处分离,设此时共同速度为v,根据动能定理有:W-2μmgx1cosθ-2mgx1sinθ=
| 1 |
| 2 |
分离后对A有:μmgx2cosθ+mgx2sinθ=
| 1 |
| 2 |
联立以上各式可得:x2=x0-
| 5v02 |
| 32μg |
答:(1)O点和O′点间的距离x1=
| 5v02 |
| 16μg |
(2)分离后物块A沿斜面向上滑行的最大距离x2是x2=x0-
| 5v02 |
| 32μg |
点评:运用动能定理解题,关键选择合适的研究过程,分析过程中有哪些力做功,然后根据动能定理列式求解.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
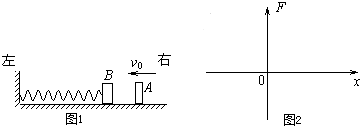
 水平地面上有一直立的轻质弹簧,下端固定\上端与物体4相连接,整个系统处于静止状态,如图1所示.现用一竖直向下的力F作用在物体4上,使4向下做一小段匀加速直线动(弹簧一直处在弹性限度内)如图2所示.在此过程中力F的大小与物体向下运动的距离x间的关系图象正确的是( )
水平地面上有一直立的轻质弹簧,下端固定\上端与物体4相连接,整个系统处于静止状态,如图1所示.现用一竖直向下的力F作用在物体4上,使4向下做一小段匀加速直线动(弹簧一直处在弹性限度内)如图2所示.在此过程中力F的大小与物体向下运动的距离x间的关系图象正确的是( )