Question

【题目】如图所示，在竖直平面内有一半径为R的圆弧轨道，半径OA水平、OB竖直，一个质量为m的小球自A的正上方P点由静止开始自由下落，小球沿轨道到达最高点B时恰好对轨道没有压力．已知AP=2R，重力加速度为g，则小球从P到B的运动过程中（ ）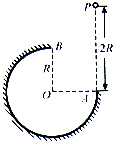

A.重力做功mgR
B.机械能减少mgR
C.合外力做功mgR
D.克服摩擦力做功0.5mgR

Answer 1

【答案】A,D
【解析】解：A、重力做功WG=mg（2R﹣R）=mgR，故A正确；
B、小球沿轨道到达最高点B时恰好对轨道没有压力，则有
mg=m ，解得：vB=
则机械能减少量为△E=mgR﹣ =0.5mgR，故B错误．
C、根据动能定理得：
合外力做功 W合= mvB2=0.5mgR，故C错误．
D、根据功能原理可知，克服摩擦力做功等于机械能的减少，为0.5mgR．故D正确．
故选：AD．
【考点精析】根据题目的已知条件，利用功能关系的相关知识可以得到问题的答案，需要掌握当只有重力（或弹簧弹力）做功时，物体的机械能守恒；重力对物体做的功等于物体重力势能的减少:W G =E p1 -E p2；合外力对物体所做的功等于物体动能的变化:W 合 =E k2 -E k1 （动能定理）；除了重力（或弹簧弹力）之外的力对物体所做的功等于物体机械能的变化:W F =E 2 -E 1．