题目内容
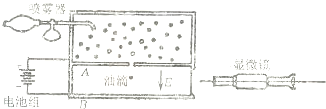
 电子所带电量最早是由美国科学家密立根通过油滴实验测出的.油滴实验的原理如下图所示,两块水平放置的平行金属板与电源连接,上、下板分别带正、负电荷.油滴从喷雾器喷出后,由于摩擦而带电,油滴进入上板中央小孔后落到匀强电场中,通过显微镜可以观察到油滴的运动情况.两金属板间的距离为d,忽略空气对油滴的浮力和阻力.
电子所带电量最早是由美国科学家密立根通过油滴实验测出的.油滴实验的原理如下图所示,两块水平放置的平行金属板与电源连接,上、下板分别带正、负电荷.油滴从喷雾器喷出后,由于摩擦而带电,油滴进入上板中央小孔后落到匀强电场中,通过显微镜可以观察到油滴的运动情况.两金属板间的距离为d,忽略空气对油滴的浮力和阻力.(1)调节两金属板间的电势差U,当u=Uo时,使得某个质量为ml的油滴恰好做匀速运动.该油滴所带电荷量q为多少?
(2)若油滴进入电场时的速度可以忽略,当两金属板间的电势差u=U时,观察到某个质量为m2的油滴进入电场后做匀加速运动,经过时间t运动到下极板.若此油滴所带的电量的电性与(1)相同,求此油滴所带电荷量Q.
分析:(1)质量为ml的油滴恰好做匀速运动,油滴受力平衡,根据所受电场力等于重力即可求解;
(2)油滴进入电场后做匀加速直线运动,根据牛顿第二定律及运动学公式列式即可求解.
(2)油滴进入电场后做匀加速直线运动,根据牛顿第二定律及运动学公式列式即可求解.
解答:解:(1)油滴匀速下落过程中受到电场力和重力平衡,此时油滴所带的电量为负电荷.
由二力平衡关系可得:q
=m1g①
由①式可得:q=m1
②
(3)油滴加速下落,由(1)可知该油滴带负电,此进它受到的电场力向,设此时的加速度大小为a1,由牛顿第二定律可得:m2g-Q1
=m2a1③
由运动学公式可得:d=
a1t12④
由③④二式可得:Q1=
(g-
)⑤
答:(1)该油滴所带电荷量q为m1
;
(2)此油滴所带电荷量Q为
(g-
).
由二力平衡关系可得:q
| U0 |
| d |
由①式可得:q=m1
| gd |
| U0 |
(3)油滴加速下落,由(1)可知该油滴带负电,此进它受到的电场力向,设此时的加速度大小为a1,由牛顿第二定律可得:m2g-Q1
| U |
| d |
由运动学公式可得:d=
| 1 |
| 2 |
由③④二式可得:Q1=
| m2d |
| U |
| 2d |
| t2 |
答:(1)该油滴所带电荷量q为m1
| gd |
| U0 |
(2)此油滴所带电荷量Q为
| m2d |
| U |
| 2d |
| t2 |
点评:该题主要考查了牛顿第二定律及匀加速直线运动位移时间公式的应用,求解出加速度是关键.

练习册系列答案
相关题目
 电子所带电荷量最早是由美国科学家密立根通过油滴实验测出的.油滴实验的原理如图所示,两块水平放置的平行金属板与电源连接,上、下板分别带正、负电荷.油滴从喷雾器喷出后,由于摩擦而带电,油滴进入上板中央小孔后落到匀强电场中,通过显微镜可以观察到油滴的运动情况.忽略空气对油滴的浮力和阻力.若两块水平放置的平行金属板板间场强大小为8.0×103N/C,两板相距0.05m,则两板电势差为
电子所带电荷量最早是由美国科学家密立根通过油滴实验测出的.油滴实验的原理如图所示,两块水平放置的平行金属板与电源连接,上、下板分别带正、负电荷.油滴从喷雾器喷出后,由于摩擦而带电,油滴进入上板中央小孔后落到匀强电场中,通过显微镜可以观察到油滴的运动情况.忽略空气对油滴的浮力和阻力.若两块水平放置的平行金属板板间场强大小为8.0×103N/C,两板相距0.05m,则两板电势差为