题目内容
4.图甲是“研究平抛物体的运动”的实验装置图.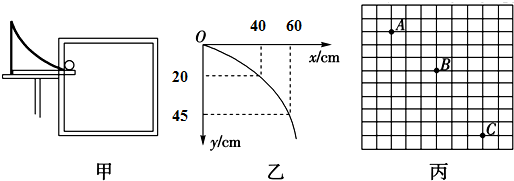
(1)实验前应对实验装置反复调节,直到斜槽末端切线水平,检验斜槽末端水平的方法是:小球放在斜槽末端任意位置不滚动.每次让小球从同一位置由静止释放,是为了每次平抛初速度相同.
(2)图乙是正确实验取得的数据,其中O为抛出点,则此小球做平抛运动的初速度为2m/s.(g取10m/s2)
(3)在另一次实验中将白纸换成方格纸,每小格的边长L=1.25cm,通过实验,记录了小球在运动途中的三个位置,如图丙所示,则该小球做平抛运动的初速度为0.75m/s;B点的竖直分速度为1m/s.(g取10m/s2)
分析 (1)平抛运动的初速度一定要水平,因此为了获得水平的初速度安装斜槽轨道时要注意槽口末端要水平;同时为了保证小球每次平抛的轨迹都是相同的,要求小球平抛的初速度相同;
(2)O点为平抛的起点,水平方向匀速x=v0t,竖直方向自由落体y=$\frac{1}{2}$gt2,据此可正确求解;
(3)根据竖直方向运动特点△h=gt2,求出物体运动时间,然后利用水平方向物体做匀速运动,可以求出其水平速度大小,利用匀变速直线运动的推论可以求出B点的竖直分速度大小.
解答 解:(1)实验前应对实验装置反复调节,直到斜槽末端切线水平,检验斜槽末端水平的方法是:小球放在斜槽末端任意位置不滚动,为了保证小球每次平抛的轨迹都是相同的,这就要求小球平抛的初速度相同,因此在操作中要求每次小球能从同一位置静止释放.
(2)由于O为抛出点,所以根据平抛运动规律有:
x=v0t
y=$\frac{1}{2}$gt2
将x=40cm=0.4m,y=20cm=0.2m,
代入解得:v0=2m/s.
(3)设相邻两点间的时间间隔为T,
竖直方向:5L-3L=gT2,
得到T=$\sqrt{\frac{2L}{g}}$=0.05s;
水平方向:v0=$\frac{3×0.0125}{0.05}$=0.75m/s;
小球在b点时,竖直方向上的瞬时速度等于vby=$\frac{3L+5L}{2T}$=1m/s
故答案为:(1)小球放在斜槽末端任意位置不滚动;初速度相同
(2)2
(3)0.75;1
点评 本题不但考查了平抛运动的规律,还灵活运用了匀速运动和匀变速运动的规律,是一道考查基础知识的好题目.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
19.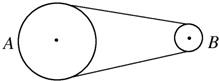 如图所示,两个皮带轮通过皮带传动(皮带与轮不发生相对滑动).大轮半径是小轮半径的2倍,设A、B分别是大小轮轮上的一点,现比较它们的线速度v、角速度ω、周期T和频率f之间的关系,正确的是( )
如图所示,两个皮带轮通过皮带传动(皮带与轮不发生相对滑动).大轮半径是小轮半径的2倍,设A、B分别是大小轮轮上的一点,现比较它们的线速度v、角速度ω、周期T和频率f之间的关系,正确的是( )
①fA:fB=1:2
②vA:vB=1:2
③TA:TB=1:2
④ωA:ωB=1:2.
 如图所示,两个皮带轮通过皮带传动(皮带与轮不发生相对滑动).大轮半径是小轮半径的2倍,设A、B分别是大小轮轮上的一点,现比较它们的线速度v、角速度ω、周期T和频率f之间的关系,正确的是( )
如图所示,两个皮带轮通过皮带传动(皮带与轮不发生相对滑动).大轮半径是小轮半径的2倍,设A、B分别是大小轮轮上的一点,现比较它们的线速度v、角速度ω、周期T和频率f之间的关系,正确的是( )①fA:fB=1:2
②vA:vB=1:2
③TA:TB=1:2
④ωA:ωB=1:2.
| A. | ②④ | B. | ③④ | C. | ①② | D. | ①④ |
9.关于摩擦力做功的下列说法中正确的是( )
| A. | 滑动摩擦力一定做负功 | |
| B. | 静摩擦力一定不做功 | |
| C. | 静摩擦力可能做功 | |
| D. | 两物体间相互作用的一对摩擦力做功的总和恒等于零 |
13.用内径很细的玻璃管做成的水银气压计,其读数比实际气压( )
| A. | 偏高 | B. | 偏低 | C. | 相同 | D. | 无法判断 |


 如图所示,用伏安法测电阻.电压表的内电阻为2.0×103Ω,电流表的内电阻为1.0×10-2Ω.已知电压表的读数为20V,电流表读数为0.4A,则待测电阻RX的测量值为50Ω,其真实值应该为51.3Ω.
如图所示,用伏安法测电阻.电压表的内电阻为2.0×103Ω,电流表的内电阻为1.0×10-2Ω.已知电压表的读数为20V,电流表读数为0.4A,则待测电阻RX的测量值为50Ω,其真实值应该为51.3Ω. 如图所示,起重机将货物沿竖直方向匀加速吊起,同时又沿横梁水平匀速向右运动.此时,站在地面上观察,货物运动的轨迹可能是下图中的哪一个?( )
如图所示,起重机将货物沿竖直方向匀加速吊起,同时又沿横梁水平匀速向右运动.此时,站在地面上观察,货物运动的轨迹可能是下图中的哪一个?( )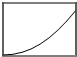



 在研究电磁感应现象的实验中所用的器材如图所示.它们是:①灵敏电流表、②蓄电池、③带铁芯的线圈A、④线圈B、⑤电键、⑥滑动变阻器(用来控制电流以改变磁场强弱).
在研究电磁感应现象的实验中所用的器材如图所示.它们是:①灵敏电流表、②蓄电池、③带铁芯的线圈A、④线圈B、⑤电键、⑥滑动变阻器(用来控制电流以改变磁场强弱).