题目内容
7.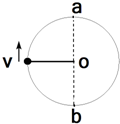 如图所示,细杆的一端与一小球相连,可绕过O点的水平轴自由转动,现给小球一初速度,使它做圆周运动,图中a、b分别表示小球转到的最低点和最高点,关于杆对球的作用力的说法正确的是( )
如图所示,细杆的一端与一小球相连,可绕过O点的水平轴自由转动,现给小球一初速度,使它做圆周运动,图中a、b分别表示小球转到的最低点和最高点,关于杆对球的作用力的说法正确的是( )| A. | a处一定为拉力,b处可能为拉力 | B. | a处为一定拉力,b处可能推力 | ||
| C. | a处可能为推力,b处一定拉力 | D. | a、b两处可能都为推力 |
分析 对小球在a、b点进行受力分析,由于小球做圆周运动,小球需要向心力.
找出小球向心力的来源,根据牛顿第二定律列出等式,判断杆对球的作用力的方向.
解答 解:过最点a时,小球做圆周运动,需要的向心力竖直向下,指向圆心.
由于轻杆能对小球可以提供支持力,也可以提供拉力,
(1)当在a点时速度0≤v<$\sqrt{gr}$时,小球的重力大于其所需的向心力,轻杆对小球有竖直向上的支持力,
(2)当在b点时速度v=$\sqrt{gr}$时,小球的重力等于其所需的向心力,轻杆对小球的作用力为0.
(3)当在b点时速度v>$\sqrt{gr}$时,小球的重力不足以提供向心力,轻杆对小球有指向圆心的拉力.
过最低点b时,小球做圆周运动,需要的向心力竖直向上,指向圆心.
根据最低点小球的合力提供向心力,那么小球只有受竖直向下的重力和竖直向上的拉力,所以a处可能为推力,可能为拉力,b处一定拉力,故ABD错误,C正确;
故选:C.
点评 轻杆的作用力可以提供支持力,也可以提供拉力,
要判断是拉力还是支持力,我们要从小球所需要得向心力入手研究,根据需要的向心力的大小和方向确定杆子的作用力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.关于人造地球卫星,下列说法中错误的是( )
| A. | 卫星运行的轨道半径越大,速度越小,运行周期越大 | |
| B. | 国家正在我省文昌市兴建第四个航天发射场.与我国原有的其他航天发射场相比较,文昌在地理位置因素的优势是纬度低.地球自转线速度大 | |
| C. | 人造卫星在升空过程中处于超重状态 | |
| D. | 人造地球同步卫星在赤道上空运行,运行一周所需的时间为一年 |
18.快热式电热水器,也叫即热电热水器,它无需巨大的储水桶,不需预热和保温.通电通水后打开出水口几秒种就会流出热水,即开、即热、即用、即停,省时、省电、省水、省空间,因此有逐渐替代储水式电热水器的趋势.如表是某快热式电热水器的铭牌,求该电热水器正常工作时:
(1)通过电热水器的电流;
(2)电热水器工作100s产生的热量.
| 快热式电热水器 | |
| 型号 | DSF-S6-80 |
| 额定电压 | 220V~ |
| 额定频率 | 50Hz |
| 额定功率 | 8800W |
| 额定压力 | 0.6Mpa |
| 防水等级 | LPX 4 |
(2)电热水器工作100s产生的热量.
2.LC回路中电容器两端电压U随时间t变化的关系如图所示,则( )
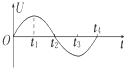

| A. | 在时刻t2,电路中的电流为零 | |
| B. | 在时刻t3,电路中的磁场能最大 | |
| C. | 从时刻t2至t3,电路中的电场能不断增大 | |
| D. | 从时刻t3至t4,电容器所带的电荷量不断增大 |
19.假设地球是一半径为R,质量分布均匀的球体.假设一矿井深度为d=$\frac{R}{2}$,已知质量分布均匀的球壳对壳内物体的引力为零.矿井底部和地面处的重力加速度大小之比为( )
| A. | 4 | B. | $\frac{1}{4}$ | C. | 2 | D. | $\frac{1}{2}$ |
16.关于永动机和热力学定律的讨论,系列叙述正确的是 ( )
| A. | 第二类永动机违反能量守恒定律 | |
| B. | 热量不可能自发地从低温物体传到高温物体 | |
| C. | 对某物体做功,物体的内能必定增加 | |
| D. | 可以从单一热源吸收热量,使之完全变为功 | |
| E. | 能量耗散从能量转化角度反映出自然界中的宏观过程具有方向性 |
17.宇航员在月球表面以初速度v0将一石块与水平方向成θ角斜向上抛出,小球上升的最大高度为h,月球的半径为R,引力常量为G.由此可推算( )
| A. | 月球表面的重力加速度为$\frac{{{v}_{0}}^{2}co{s}^{2}θ}{2h}$ | |
| B. | 月球的质量为$\frac{{{v}_{0}}^{2}{R}^{2}si{n}^{2}θ}{2Gh}$ | |
| C. | 石块在空中的运动时间为$\frac{2h}{{v}_{0}sinθ}$ | |
| D. | 月球的第一宇宙速度为v0sinθ$\sqrt{\frac{R}{h}}$ |
 如图所示,在xOy坐标平面内,直线MN为区域足够大的匀强电场和匀强磁场的分界线,MN的右上方分布着垂直于坐标平面向里、磁感应强度大小为B的匀强磁场,MN的左下方分布着沿y轴负方向的匀强电场,MN过原点O且与x轴成θ=45°.从O点分别沿x轴、y轴正方向同时发射一正、负电子,初速度大小分别为v、2v.已知正、负电子的质量均为m,电量分别为+e和-e,忽略正、负电子之间的作用力及重力,求:
如图所示,在xOy坐标平面内,直线MN为区域足够大的匀强电场和匀强磁场的分界线,MN的右上方分布着垂直于坐标平面向里、磁感应强度大小为B的匀强磁场,MN的左下方分布着沿y轴负方向的匀强电场,MN过原点O且与x轴成θ=45°.从O点分别沿x轴、y轴正方向同时发射一正、负电子,初速度大小分别为v、2v.已知正、负电子的质量均为m,电量分别为+e和-e,忽略正、负电子之间的作用力及重力,求: 一位质量m=50kg的滑雪运动员(包括滑雪板)从高度h=30m的斜坡自由滑下(初速度为零).斜坡的倾角θ=37°,滑雪板与雪面滑动摩擦因素μ=0.1.(不计空气阻力)则运动员(包括滑雪板)滑至坡底的过程中(g取10m/s2,sin37°=0.6,cos37°=0.8)
一位质量m=50kg的滑雪运动员(包括滑雪板)从高度h=30m的斜坡自由滑下(初速度为零).斜坡的倾角θ=37°,滑雪板与雪面滑动摩擦因素μ=0.1.(不计空气阻力)则运动员(包括滑雪板)滑至坡底的过程中(g取10m/s2,sin37°=0.6,cos37°=0.8)