��Ŀ����
��ͼ��ʾ��ˮƽ���õ�ƽ�н�����A��D��ľ���Ϊd�������峤ΪL=
d����������ӵ�ѹΪU��D����Ҳ��Եǡ������б����NM�ϵ�һ��С��K��NM��ˮƽ����NP��60��ǣ��ҵ����㹻����K��N��ľ���ΪKN=a������һ����Ϊm�������Ϊq�Ĵ���������ӣ���A��D���е�O��ƽ���ڽ����巽��OO'��ijһ�ٶ����룬�������ӵ������������Ӵ����������ǡ�ô�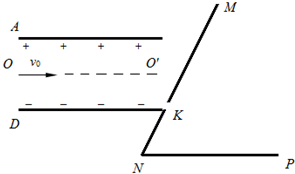 ��С��K��
����K��
��1��������Ӵ�O������ʱ���ٶȴ�Сv0��
��2�������������е������������һ��ֱֽ���������ǿ�ų������Ӿ����ų�ƫת���ܴ�ֱ����ˮƽ����NP�ϣ���ôų��ĴŸ�Ӧǿ�ȵĴ�СB0��
��3�����ų������Ϊ��ֱֽ�������ֻ���������������м��ijһ�����ڣ�ͬ��ʹ�����Ӿ����ų�ƫת���ܴ�ֱ����ˮƽ����NP�ϣ�֮ǰ�뵲��û����ײ���������������ĴŸ�Ӧǿ�ȵ���СֵBmin��
| 3 |
 ����K��
��С��K����1��������Ӵ�O������ʱ���ٶȴ�Сv0��
��2�������������е������������һ��ֱֽ���������ǿ�ų������Ӿ����ų�ƫת���ܴ�ֱ����ˮƽ����NP�ϣ���ôų��ĴŸ�Ӧǿ�ȵĴ�СB0��
��3�����ų������Ϊ��ֱֽ�������ֻ���������������м��ijһ�����ڣ�ͬ��ʹ�����Ӿ����ų�ƫת���ܴ�ֱ����ˮƽ����NP�ϣ�֮ǰ�뵲��û����ײ���������������ĴŸ�Ӧǿ�ȵ���СֵBmin��
��1�������ڵ糡������ƽ���˶���L=v0t
=
at2
a=
���룺L=
d
�ɵã�v0=
��2������������ڽ���Kʱ��ֱ����ķ��ٶ�Ϊvy
ˮƽ����L=
d=v0t
��ֱ����
=
t
�ɵã�tan��=
=
������=30�㣬
���ӵ���K��ʱ�ٶ�Ϊ��v=2
�ɼ��ι�ϵ�ɵã�����Բ���˶��뾶Ϊr=a
�����㣺qB0v=
�ɵã�B0=
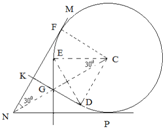
��3���ų�������ͼ�����Ӵ�K�������������ֱ���˶���D�㿪ʼ����ų������ݶԳ��ԣ���ƫת300����E�������������ֱ���˶���ֱ��NP�����ϣ�
���ݣ�Bqv=m
�ɵã�B=
ҪʹB��С������ʹ�뾶r����ٽ�����ǹ켣�պú͵�������
�ɼ��ι�ϵ�ɵã�
r=a+r
�ɵã�r=
��ã�Bmin=
�𣺣�1�������Ӵ�O������ʱ���ٶȴ�СΪ
��
��2���ôų��ĴŸ�Ӧǿ�ȵĴ�СΪ
��
��3�����������ĴŸ�Ӧǿ�ȵ���СֵΪ
��
| d |
| 2 |
| 1 |
| 2 |
a=
| qU |
| dm |
���룺L=
| 3 |
�ɵã�v0=
|
��2������������ڽ���Kʱ��ֱ����ķ��ٶ�Ϊvy
ˮƽ����L=
| 3 |
��ֱ����
| d |
| 2 |
| vy |
| 2 |
�ɵã�tan��=
| vy |
| v0 |
| ||
| 3 |
���ӵ���K��ʱ�ٶ�Ϊ��v=2
|
�ɼ��ι�ϵ�ɵã�����Բ���˶��뾶Ϊr=a
�����㣺qB0v=
| mv2 |
| r |
�ɵã�B0=
| 2 |
| a |
|
��3���ų�������ͼ�����Ӵ�K�������������ֱ���˶���D�㿪ʼ����ų������ݶԳ��ԣ���ƫת300����E�������������ֱ���˶���ֱ��NP�����ϣ�

���ݣ�Bqv=m
| v2 |
| r |
| mv |
| qr |
ҪʹB��С������ʹ�뾶r����ٽ�����ǹ켣�պú͵�������
�ɼ��ι�ϵ�ɵã�
| 3 |
�ɵã�r=
| a | ||
|
��ã�Bmin=
2(
| ||
| a |
|
�𣺣�1�������Ӵ�O������ʱ���ٶȴ�СΪ
|
��2���ôų��ĴŸ�Ӧǿ�ȵĴ�СΪ
| 2 |
| a |
|
��3�����������ĴŸ�Ӧǿ�ȵ���СֵΪ
2(
| ||
| a |
|

��ϰ��ϵ�д�
�����Ŀ