题目内容
如图(甲)所示,弯曲部分AB和CD是两个半径相等的四分之一圆弧,中间的BC段是竖直的薄壁细圆管(细圆管内径略大于小球的直径),分别与上、下圆弧轨道相切连接,BC段的长度L可作伸缩调节。下圆弧轨道与地面相切,其中D、A分别是上、下圆弧轨道的最高点与最低点,整个轨道固定在竖直平面内。一小球多次以某一速度从A点水平进入轨道而从D点水平飞出。今在A、D两点各放一个压力传感器,测试小球对轨道A、D两点的压力,计算出压力差△F。改变BC间距离L,重复上述实验,最后绘得△F-L的图线如图(乙)所示。(不计一切摩擦阻力,g取10m/s2)
(1)某一次调节后D点离地高度为0.8m。小球从D点飞出,落地点与D点水平距离为2.4m,求小球过D点时速度大小。
 (2)求小球的质量和弯曲圆弧轨道的半径大小。
(2)求小球的质量和弯曲圆弧轨道的半径大小。
(1)6m/s (2) 0.4m
解析:
⑴小球在竖直方向做自由落体运动,![]()
水平方向做匀速直线运动 ![]()
得: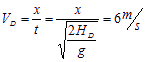
⑵设轨道半径为r,A到D过程机械能守恒:
![]()
在A点:![]()
在D点:![]()
由以上三式得:
![]()
由图象纵截距得:6mg=12 得m=0.2kg
由L=0.5m时 △F=17N
代入得:
r=0.4m

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
 圆弧,中间的BC段是竖直的薄壁细圆管(细圆管内径略大于小球的直径),细圆管分别与上、下圆弧轨道相切连接,BC段的长度L可作伸缩调节。下圆弧轨道与地面相切,其中D、A分别是上、下圆弧轨道的最高点与最低点,整个轨道固定在竖直平面内。一小球多次以某一速度从A点水平进入轨道而从D点水平飞出。今在A、D两点各放一个压力传感器,测试小球对轨道A、D两点的压力,计算出压力差△F。改变BC间距离L,重复上述实验,最后绘得
圆弧,中间的BC段是竖直的薄壁细圆管(细圆管内径略大于小球的直径),细圆管分别与上、下圆弧轨道相切连接,BC段的长度L可作伸缩调节。下圆弧轨道与地面相切,其中D、A分别是上、下圆弧轨道的最高点与最低点,整个轨道固定在竖直平面内。一小球多次以某一速度从A点水平进入轨道而从D点水平飞出。今在A、D两点各放一个压力传感器,测试小球对轨道A、D两点的压力,计算出压力差△F。改变BC间距离L,重复上述实验,最后绘得 的图线如图(乙)所示,(不计一切摩擦阻力,g取10m/s2),试求:
的图线如图(乙)所示,(不计一切摩擦阻力,g取10m/s2),试求:
 圆弧,中间的BC段是竖直的薄壁细圆管(细圆管内径略大于小球的直径),细圆管分别与上、下圆弧轨道相切连接,BC段的长度L可作伸缩调节。下圆弧轨道与地面相切,其中D、A分别是上、下圆弧轨道的最高点与最低点,整个轨道固定在竖直平面内。一小球多次以某一速度从A点水平进入轨道而从D点水平飞出。今在A、D两点各放一个压力传感器,测试小球对轨道A、D两点的压力,计算出压力差△F。改变BC间距离L,重复上述实验,最后绘得
圆弧,中间的BC段是竖直的薄壁细圆管(细圆管内径略大于小球的直径),细圆管分别与上、下圆弧轨道相切连接,BC段的长度L可作伸缩调节。下圆弧轨道与地面相切,其中D、A分别是上、下圆弧轨道的最高点与最低点,整个轨道固定在竖直平面内。一小球多次以某一速度从A点水平进入轨道而从D点水平飞出。今在A、D两点各放一个压力传感器,测试小球对轨道A、D两点的压力,计算出压力差△F。改变BC间距离L,重复上述实验,最后绘得 的图线如图(乙)所示,(不计一切摩擦阻力,g取10m/s2),试求:
的图线如图(乙)所示,(不计一切摩擦阻力,g取10m/s2),试求: