题目内容
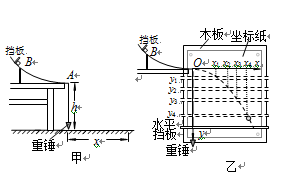
如图甲所示,水平桌面的左端固定一竖直放置的光滑圆弧轨道,其半径R=0.5m,圆弧轨道底端与水平桌面相切于C点,桌面CD长L=1m,高h2=0.5m,有质量为m(m为未知)的小物块从圆弧上A点由静止释放,A点距桌面的高度h1=0.2m,小物块经过圆弧轨道底端滑到桌面CD上,在桌面CD上运动时始终受到一个水平向右的恒力F作用。然后从D点飞出做平抛运动,最后落到水平地面上。设小物块从D点飞落到水平地面上的水平距离为x,如图乙是x2—F的图象,取重力加速度g=10m/s2。
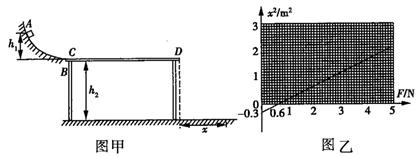
(1)试写出小物块经D点时的速度vD与x的关系表达式。
(2)小物块与水平桌面CD间动摩擦因数μ是多少?
(3)若小物块与水平桌面CD间动摩擦因数μ是从第(2)问中的值开始由C到D均匀减小,且在D点恰好减小为0。再将小物块从A由静止释放,经过D点滑出后的水平位移大小为1m,求此情况下的恒力F的大小。
(1)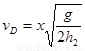 (2)0.35(3)1.9N
(2)0.35(3)1.9N
【解析】
试题分析:⑴物体从D滑出后做平抛运动,则
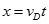 …………………………………………………(2分)
…………………………………………………(2分)
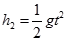 ……………………………………………………(2分)
……………………………………………………(2分)
入化简可得 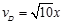 或
或
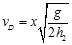 …………………(1分)
…………………(1分)
⑵由A→D全程动能定理得
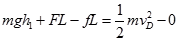 ………………………………(2分)
………………………………(2分)
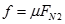
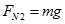 …………………………… (1分)
…………………………… (1分)
代入整理得 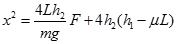 ………………(1分)
………………(1分)
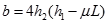 ………………………………(1分)
………………………………(1分)
由图可知 b =-0.3
代入计算可得 μ=0.35 …………………………………………(1分)
⑶由第(2)可知 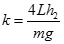 ……………………………(1分)
……………………………(1分)
由乙图可知 k ="0." 5
代入计算得
m =0.4kg …………………………………………(1分)
由A→D全程动能定理得
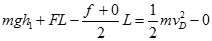 ……………………(2分)
……………………(2分)
由题可知:x=1m
由第(1)问知
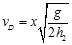
则代入计算得 F=1.9N ……………………………………………(1分
考点:考查了平抛运动和功能定理的应用
点评:该题涉及到多个运动过程,主要考查了动能定理、平抛运动基本公式应用,用到的知识点及公式较多,难度较大,属于难题.

 阅读快车系列答案
阅读快车系列答案 如图甲所示,水平桌面上固定有一位于竖直平面内的弧形轨道A,其下端的切线是水平的,轨道的厚度可忽略不计.将小铁块B从轨道的固定挡板处由静止释放,小铁块沿轨道下滑,最终落到水平地面上.若测得轨道末端距离水平地面的高度为h,小铁块从轨道飞出到落地的水平位移为x,已知当地的重力加速度为g.
如图甲所示,水平桌面上固定有一位于竖直平面内的弧形轨道A,其下端的切线是水平的,轨道的厚度可忽略不计.将小铁块B从轨道的固定挡板处由静止释放,小铁块沿轨道下滑,最终落到水平地面上.若测得轨道末端距离水平地面的高度为h,小铁块从轨道飞出到落地的水平位移为x,已知当地的重力加速度为g.