题目内容
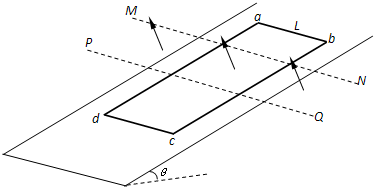
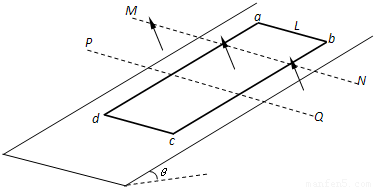
如图所示,N匝矩形金属线圈的质量为m,电阻为R,放在倾角为θ的光滑斜面上,其ab边长度为L且与斜面底边平行.与ab平行的两水平虚线MN、PQ之间,在t=0时刻加一变化的磁场,磁感应强度B大小随时间t的变化关系为B=Kt,方向垂直斜面向上.在t=0时刻将线圈由图中位置静止释放,在t=t1时刻ab边进入磁场,t=t2时刻ab边穿出磁场.线圈ab边刚进入磁场瞬间电流为0,穿出磁场前的瞬间线圈加速度为0.(重力加速度为g)求: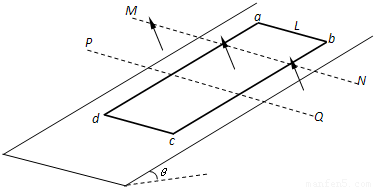
(1)MN、PQ之间的距离d;
(2)从t=0到t=t1运动过程中线圈产生的热量Q;
(3)线圈的ab边在穿过磁场过程中克服安培力所做的功W.
【答案】分析:(1)ab边进入磁场前,线圈做匀加速运动,由牛顿第二定律可以求出线圈的加速度,由匀变速运动的速度公式求出ab边进入磁场时的速度;由法拉第电磁定律求出由于磁场变化而产生的感应电动势,由E=BLv求出ab切割磁感线而产生的感应电动势,由题意知,这两个电动势的和电动势是零,据此求出磁场的宽度d.
(2)由欧姆定律求出感应电流,由焦耳定律求出焦耳热.
(3)线圈穿出磁场时的加速度为零,合力为零,求出此时线圈受到的安培力,由平衡条件求出线圈穿出磁场时的速度,然后由动能定理求出安培力所做的功.
解答:解:(1)线圈进入磁场前做匀加速运动,
由牛顿第二定律得:mgsinθ=ma,a=gsinθ,
当t=t1时,线圈的速度:v1=at1=gsinθt1…①
由法拉第电磁感应定律得,由于磁场变化产生的感应电动势:
E1=N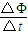 =NS
=NS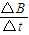 =Ndl
=Ndl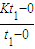 =NKld,
=NKld,
ab边切割磁感线产生的感应电动势:
E1′=NB1lv1=NKlgt12sinθ,
由题意可知瞬间电流为0,
则:E合=E1-E1′=0
即:NKdl=NKlgt12sinθ,
∴磁场宽度:d=gt12sinθ;
(2)由(1)可知:E1=NKld,感应电流:I=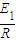 =
=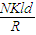 ,
,
从t=0到t=t1运动过程中线圈产生的热量Q:
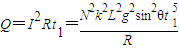 ;
;
(3)当t=t2时,由题意知:mgsinθ-NB2I2L=0,
设ab边穿出磁场瞬间的速度为v2,
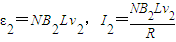 ,
,
∴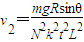 ,
,
由动能定理: ,
,
解得: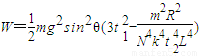 ;
;
答:(1)MN、PQ之间的距离为gt12sinθ;
(2)从t=0到t=t1运动过程中线圈产生的热量为 ;
;
(3)线圈的ab边在穿过磁场过程中克服安培力所做的功为 mg2sin2θ
mg2sin2θ .
.
点评:分析清楚线圈的运动过程、对线圈正确受力分析、熟练应用法拉第电磁感应定律、动能定律是正确解题的关键,本题计算量大,过程较复杂,是一道难题,解题是要细心、认真,否则会出错.
(2)由欧姆定律求出感应电流,由焦耳定律求出焦耳热.
(3)线圈穿出磁场时的加速度为零,合力为零,求出此时线圈受到的安培力,由平衡条件求出线圈穿出磁场时的速度,然后由动能定理求出安培力所做的功.
解答:解:(1)线圈进入磁场前做匀加速运动,
由牛顿第二定律得:mgsinθ=ma,a=gsinθ,
当t=t1时,线圈的速度:v1=at1=gsinθt1…①
由法拉第电磁感应定律得,由于磁场变化产生的感应电动势:
E1=N
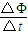 =NS
=NS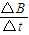 =Ndl
=Ndl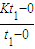 =NKld,
=NKld,ab边切割磁感线产生的感应电动势:
E1′=NB1lv1=NKlgt12sinθ,
由题意可知瞬间电流为0,
则:E合=E1-E1′=0
即:NKdl=NKlgt12sinθ,
∴磁场宽度:d=gt12sinθ;
(2)由(1)可知:E1=NKld,感应电流:I=
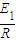 =
=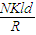 ,
,从t=0到t=t1运动过程中线圈产生的热量Q:
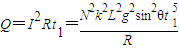 ;
;(3)当t=t2时,由题意知:mgsinθ-NB2I2L=0,
设ab边穿出磁场瞬间的速度为v2,
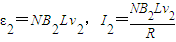 ,
,∴
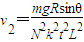 ,
,由动能定理:
 ,
,解得:
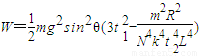 ;
;答:(1)MN、PQ之间的距离为gt12sinθ;
(2)从t=0到t=t1运动过程中线圈产生的热量为
 ;
;(3)线圈的ab边在穿过磁场过程中克服安培力所做的功为
 mg2sin2θ
mg2sin2θ .
.点评:分析清楚线圈的运动过程、对线圈正确受力分析、熟练应用法拉第电磁感应定律、动能定律是正确解题的关键,本题计算量大,过程较复杂,是一道难题,解题是要细心、认真,否则会出错.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

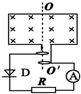 如图所示,N匝矩形导线框以角速度ω在磁感应强度为B的匀强磁场中绕轴OO′匀速转动,线框面积为S,线框的电阻、电感均不计,外电路接有电阻R、理想交流电流表
如图所示,N匝矩形导线框以角速度ω在磁感应强度为B的匀强磁场中绕轴OO′匀速转动,线框面积为S,线框的电阻、电感均不计,外电路接有电阻R、理想交流电流表 和二极管D,二极管D具有单向导电性,即正向电阻为零,反向电阻无穷大.下列说法正确的是( )
和二极管D,二极管D具有单向导电性,即正向电阻为零,反向电阻无穷大.下列说法正确的是( )