题目内容
4. 竖直放置的一对平行金属板的左极板上,用长为L的轻质绝缘细线悬挂一个带电量为q质量为 m的小球,将平行金属板按如图所示的电路图连接.当滑动变阻器R在a位置时,绝缘线与左极板的夹角为θ1=30°,当将滑片缓慢地移动到b位置时,夹角为θ2=60°.两板间的距离大于L,重力加速度为g.问:
竖直放置的一对平行金属板的左极板上,用长为L的轻质绝缘细线悬挂一个带电量为q质量为 m的小球,将平行金属板按如图所示的电路图连接.当滑动变阻器R在a位置时,绝缘线与左极板的夹角为θ1=30°,当将滑片缓慢地移动到b位置时,夹角为θ2=60°.两板间的距离大于L,重力加速度为g.问:(1)小球在上述两个平衡位置时,平行金属板上所带电荷量之比Q1:Q2=1:3.
(2)若保持变阻器滑片位置在a处不变,对小球再施加一个拉力,使绝缘线与竖直方向的夹角从θ1=30°缓慢地增大到θ2=60°,则此过程中拉力做的功W=$(\frac{2\sqrt{3}}{3}-1)mgL$.
分析 (1)对小球受力分析,根据共点力平衡条件得到电场力和重力之间的关系,也就知道了场强和重力之间的关系,再根据匀强电场的场强与电势差的关系,然后结合C=$\frac{Q}{U}$
计算比值即可.
(2)从30度到60度过程中,小球受到重力、电场力、绳子的拉力和外界的拉力,其中绳子的拉力不做功,其它力都做功,由于是缓慢变化,动能不变,全过程运用动能定理,列式求解拉力做功.
解答 解:(1)小球处于静止状态,受力情况如图所示,由平衡条件得: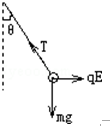 qE=mgtanθ,
qE=mgtanθ,
设两极板间的距离为d,则有:
U=Ed,C=$\frac{Q}{U}$
所以在两个平衡位置时,平行金属板上所带电荷量之比:
Q1:Q2=1:3
(2)设该过程拉力对小球做功W,用动能定理得:
W+qEl(sin60°-sin30°)-mgl(cos30°-cos60°)=0
又 qE=mgtan30°
解得:$W=(\frac{2\sqrt{3}}{3}-1)mgL$
故答案为:1:3,$(\frac{2\sqrt{3}}{3}-1)mgL$
点评 本题综合考查电路知识、匀强电场及共点力的平衡和动能定理等知识,要求学生能通过读图和审题找出其中的关系.综合能力要求较高,是一道好题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.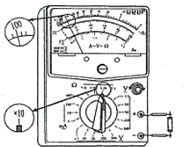 某同学测量一只未知阻值的电阻,他先用多用电表进行测量,按照正确的步骤操作后,测量的结果如图所示,为了使多用电表测量的结果更准确,该同学应该进行哪些操作( )
某同学测量一只未知阻值的电阻,他先用多用电表进行测量,按照正确的步骤操作后,测量的结果如图所示,为了使多用电表测量的结果更准确,该同学应该进行哪些操作( )
 某同学测量一只未知阻值的电阻,他先用多用电表进行测量,按照正确的步骤操作后,测量的结果如图所示,为了使多用电表测量的结果更准确,该同学应该进行哪些操作( )
某同学测量一只未知阻值的电阻,他先用多用电表进行测量,按照正确的步骤操作后,测量的结果如图所示,为了使多用电表测量的结果更准确,该同学应该进行哪些操作( )| A. | 欧姆档换成×100,再次测量 | B. | 欧姆档换成×100,调零后再次测量 | ||
| C. | 欧姆档换成×1,再次测量 | D. | 欧姆档换成×1,调零后再次测量 |
19.在一阻值为R=10Ω的定值电阻中通入如图所示的交流电,则( )


| A. | 此交流电的频率为0.5Hz | B. | 此交流电的有效值为$\frac{5}{2}$$\sqrt{2}$A | ||
| C. | 在0~2s内电阻产生的焦耳热为25J | D. | 在2~4s内通过该电阻的电荷量为1C |
9. 如图所示,质量为m的物体与倾斜角为θ的斜劈间的动摩擦因数为μ,在斜劈水平向右以加速度a匀加速移动L的过程中,物块均与斜劈保持相对静止,则( )
如图所示,质量为m的物体与倾斜角为θ的斜劈间的动摩擦因数为μ,在斜劈水平向右以加速度a匀加速移动L的过程中,物块均与斜劈保持相对静止,则( )
 如图所示,质量为m的物体与倾斜角为θ的斜劈间的动摩擦因数为μ,在斜劈水平向右以加速度a匀加速移动L的过程中,物块均与斜劈保持相对静止,则( )
如图所示,质量为m的物体与倾斜角为θ的斜劈间的动摩擦因数为μ,在斜劈水平向右以加速度a匀加速移动L的过程中,物块均与斜劈保持相对静止,则( )| A. | 弹力对物块做功等于-$\frac{1}{2}$mgLsin2θ | |
| B. | 摩擦力对物体所做的功为$\frac{1}{2}$mgLsin2θ | |
| C. | 摩擦力对物体所做的功为μmgLcos2θ | |
| D. | 弹力和摩擦力对物块做的总功为maL |
13. 如图所示,两平行金属板竖直放置且B板接地,期间有用绝缘细线悬挂的带电小球,当给两金属板充电,使金属板带电荷量为Q,此时悬线与竖直方向的夹角为$\frac{π}{3}$,因电离作用,两金属板的电荷量缓慢减小(假设小球的电荷量不变),以致悬线与竖直方向夹角逐渐减小,则夹角减小到$\frac{π}{6}$的过程中,下列说法正确的是( )
如图所示,两平行金属板竖直放置且B板接地,期间有用绝缘细线悬挂的带电小球,当给两金属板充电,使金属板带电荷量为Q,此时悬线与竖直方向的夹角为$\frac{π}{3}$,因电离作用,两金属板的电荷量缓慢减小(假设小球的电荷量不变),以致悬线与竖直方向夹角逐渐减小,则夹角减小到$\frac{π}{6}$的过程中,下列说法正确的是( )
 如图所示,两平行金属板竖直放置且B板接地,期间有用绝缘细线悬挂的带电小球,当给两金属板充电,使金属板带电荷量为Q,此时悬线与竖直方向的夹角为$\frac{π}{3}$,因电离作用,两金属板的电荷量缓慢减小(假设小球的电荷量不变),以致悬线与竖直方向夹角逐渐减小,则夹角减小到$\frac{π}{6}$的过程中,下列说法正确的是( )
如图所示,两平行金属板竖直放置且B板接地,期间有用绝缘细线悬挂的带电小球,当给两金属板充电,使金属板带电荷量为Q,此时悬线与竖直方向的夹角为$\frac{π}{3}$,因电离作用,两金属板的电荷量缓慢减小(假设小球的电荷量不变),以致悬线与竖直方向夹角逐渐减小,则夹角减小到$\frac{π}{6}$的过程中,下列说法正确的是( )| A. | 细线的拉力逐渐增大 | B. | 细线的拉力大小不变 | ||
| C. | 电容器减少的电荷量为$\frac{Q}{2}$ | D. | 电容器减少的电荷量为$\frac{2Q}{3}$ |
14.两个完全相同的金属球A和B,A带正电位3q,B带负电-q,两金属球相距r,它们间的库仑力为F1;将两球接触一下再分开,距离保持不变,它们间的库仑力为F2,则( )
| A. | F1=F2 | B. | F1=3F2 | C. | 2F1=F2 | D. | 2F1=3F2 |
 “探究功与速度变化的关系”的实验如图所示,当小车在一条橡皮筋作用下弹出时,橡皮筋对小车做的功记为W.当用2条、3条…完全相同的橡皮筋并在一起进行第2次、第3次…实验时,使每次实验中橡皮筋伸长的长度都保持一致,并打出每次实验的纸带.请将下列步骤填写完整:
“探究功与速度变化的关系”的实验如图所示,当小车在一条橡皮筋作用下弹出时,橡皮筋对小车做的功记为W.当用2条、3条…完全相同的橡皮筋并在一起进行第2次、第3次…实验时,使每次实验中橡皮筋伸长的长度都保持一致,并打出每次实验的纸带.请将下列步骤填写完整:

