题目内容
13．
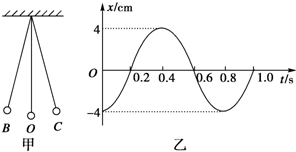图甲是一个单摆振动的情形，O是它的平衡位置，B、C是摆球所能到达的最远位置．设摆球向右方向运动为正方向．图乙是这个单摆的振动图象．根据图象回答：（1）单摆振动的频率是多大？在0时刻摆球在哪个位置？
（2）若当地的重力加速度为10m/s2，试求这个摆的摆长是多少？
分析 （1）单摆做简谐运动，完成一次全振动的时间为一个周期，图上相邻两个最大值之间的时间间隔为一个周期．由图象求出单摆的周期，然后求出频率．
根据图象所示t=0s时摆球的位移确定摆球开始时刻的位置．
（2）已知单摆周期与当地的重力加速度，由单摆周期公式的变形公式可以求出摆长．
解答 解：（1）由图乙所示图象可知，单摆周期T=0.8s，
单摆的频率：f=$\frac{1}{T}$=$\frac{1}{0.8s}$=1.25Hz．
由图乙所示图象可知，在t=0s时，摆球处于负的最大位移，摆球向右方向运动为正方向，因此开始时，摆球在B处．
（2）由单摆周期公式T=2π$\sqrt{\frac{L}{g}}$，
可得：L=$\frac{g{T}^{2}}{4{π}^{2}}$=$\frac{10×0．{8}^{2}}{4×3.1{4}^{2}}$≈0.16m；
答：（1）单摆振动的频率是0.625Hz；开始时刻摆球在B位置．
（2）若当地的重力加速度为10m/s2，这个摆的摆长是0.16m．
点评 本题考查基本的读图能力．对于简谐运动的图象，表示是振动质点相对于平衡位置的位移随时间的变化情况，可直接读出周期、振幅和速度、加速度的方向及其变化情况．
练习册系列答案
相关题目
3．
如图所示，用细线挂一质量为M的木块，有一质量为m的子弹自左向右水平射穿此木块，穿透前后子弹的速度分别为v0和v（设子弹穿过木块的时间和空气阻力不计），木块的速度大小为（ ）
如图所示，用细线挂一质量为M的木块，有一质量为m的子弹自左向右水平射穿此木块，穿透前后子弹的速度分别为v0和v（设子弹穿过木块的时间和空气阻力不计），木块的速度大小为（ ）| A． | $\frac{（m{v}_{0}+mv）}{M}$ | B． | $\frac{（m{v}_{0}-mv）}{M}$ | C． | $\frac{（m{v}_{0}+mv）}{（M+m）}$ | D． | $\frac{（m{v}_{0}-mv）}{（M+m）}$ |
4．
如图所示，一轻绳通过无摩擦的小定滑轮O与小球B连接，另一端与套在光滑竖直杆上的小物块A连接，杆两端固定且足够长，物块A由静止从图示位置释放后，先沿杆向上运动．设某时刻物块A运动的速度大小为VA，小球B运动的速度大小为VB，轻绳与杆的夹角为θ．则（ ）
如图所示，一轻绳通过无摩擦的小定滑轮O与小球B连接，另一端与套在光滑竖直杆上的小物块A连接，杆两端固定且足够长，物块A由静止从图示位置释放后，先沿杆向上运动．设某时刻物块A运动的速度大小为VA，小球B运动的速度大小为VB，轻绳与杆的夹角为θ．则（ ）| A． | vA=vBcosθ | |
| B． | vB=vAcosθ | |
| C． | 当物块A上升到与滑轮等高时，它的机械能最大 | |
| D． | 小球B减少的势能等于物块A增加的动能 |
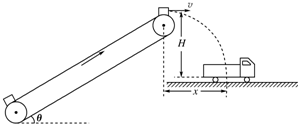如图是利用传送带装运煤块的示意图．传送带倾角θ=37°，煤块与传送带间的动摩擦因数μ=0.8，传送带的主动轮和从动轮半径相等，主动轮轴顶端与运煤车底板间的竖起高度H=1.8m，传送带底端到顶端的长度L=9m，与运煤车车箱中心的水平距离x=1.2m．现在传送带底端由静止释放一些煤块（可视为质点），煤块在传送带的作用下先做匀加速直线运动，后与传送带一起做匀速运动，到达主动轮时随轮一起匀速转动．要使煤块在轮的最高点水平抛出并落在车箱中心（ g=10m/s2，sin 37°=0.6，cos 37°=0.8）
18．篮球运动员通常要伸出两臂迎接传来的篮球．接球时，两臂随球迅速收缩至胸前．这样做可以（ ）
| A． | 减小球对手的冲量 | B． | 减小球的动量变化量 | ||
| C． | 减小球对人的冲击力 | D． | 减小球的能量变化量 |
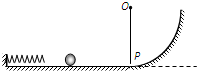如图所示，光滑水平轨道与光滑圆弧轨道相切，轻弹簧的一端固定在轨道的左端，OP是可绕O转动的轻杆，且摆到某处即能停在该处；另有一小钢球．现要利用这些器材测定弹簧被压缩一定量时的弹性势能：（ 重力加速度为g ）