题目内容
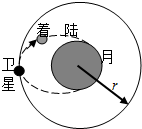 中国计划在2017年实现返回式月球软着陆器对月球进行科学探测,如图所示.届时发射一颗运动半径为r的绕月卫星,登月着陆器从绕月卫星出发,沿椭圆轨道降落到月球的表面上,与月球表面经多次碰撞和弹跳才停下来.假设着陆器第一次弹起的最大高度为h,水平速度为v1,第二次着陆时速度为v2.已知月球半径为R,着陆器质量为m,不计一切阻力和月球的自转.求:
中国计划在2017年实现返回式月球软着陆器对月球进行科学探测,如图所示.届时发射一颗运动半径为r的绕月卫星,登月着陆器从绕月卫星出发,沿椭圆轨道降落到月球的表面上,与月球表面经多次碰撞和弹跳才停下来.假设着陆器第一次弹起的最大高度为h,水平速度为v1,第二次着陆时速度为v2.已知月球半径为R,着陆器质量为m,不计一切阻力和月球的自转.求:(1)月球表面的重力加速度g月.
(2)在月球表面发射一颗月球卫星的最小发射速度是多大?
(3)设想软着陆器完成了对月球的科学考察任务后,再返回绕月卫星,返回与卫星对接时,二者具有相同的速度,着陆器在返回过程中需克服月球引力做功W=mg月(1-
| R | r |
分析:(1)着陆器在从高度为h到第二次着陆的过程中机械能守恒,根据机械能守恒定律求出月球表面的重力加速度.
(2)当卫星贴近月球表面飞行时,此时的发射速度最小,根据万有引力提供向心力,求出最小的发射速度.
(3)根据万有引力提供向心力和万有引力等于重力求出卫星在半径为r的轨道上的速度,再通过能量守恒定律求出着陆器的发动机应对着陆器做功的大小.
(2)当卫星贴近月球表面飞行时,此时的发射速度最小,根据万有引力提供向心力,求出最小的发射速度.
(3)根据万有引力提供向心力和万有引力等于重力求出卫星在半径为r的轨道上的速度,再通过能量守恒定律求出着陆器的发动机应对着陆器做功的大小.
解答:解:(1)着陆器从高度为h到第二次着陆,由机械能守恒有:mg月h-
mv12=
mv22
得出月球表面的重力加速度为:g月=
①
(2)当卫星的轨道半径为月球半径R时,发射速度最小,
设最小速度为v,由万有引力提供向心力有:m卫g月=
②
由①②式可得出:v=
(3)着陆器与卫星的对接速度为v3,对绕月卫星由牛顿定律有:
=
又在月球表面有:
=mg月
着陆器与卫星的对接时,发动机对着陆器所做的功E,由能量守恒有:E=W+
mv32=mg月(1-
)+
mv32
联立①④⑤⑥得出:E=mg月(1+
)=m
(1+
)
答:
1)月球表面的重力加速度g月=
.
(2)在月球表面发射一颗月球卫星的最小发射速度是v=
(3)陆器的电池应提供给着陆器能量为E=m
(1+
),才能使着陆器安全返回到绕月卫星.
| 1 |
| 2 |
| 1 |
| 2 |
得出月球表面的重力加速度为:g月=
| v22-v12 |
| 2h |
(2)当卫星的轨道半径为月球半径R时,发射速度最小,
设最小速度为v,由万有引力提供向心力有:m卫g月=
| m卫v2 |
| R |
由①②式可得出:v=
|
(3)着陆器与卫星的对接速度为v3,对绕月卫星由牛顿定律有:
| GM月m卫 |
| r2 |
| m卫v32 |
| r |
又在月球表面有:
| GM月m卫 |
| r2 |
着陆器与卫星的对接时,发动机对着陆器所做的功E,由能量守恒有:E=W+
| 1 |
| 2 |
| R |
| r |
| 1 |
| 2 |
联立①④⑤⑥得出:E=mg月(1+
| R2-2R |
| 2r |
| v22-v12 |
| 2h |
| R2-2R |
| 2r |
答:
1)月球表面的重力加速度g月=
| v22-v12 |
| 2h |
(2)在月球表面发射一颗月球卫星的最小发射速度是v=
|
(3)陆器的电池应提供给着陆器能量为E=m
| v22-v12 |
| 2h |
| R2-2R |
| 2r |
点评:本题综合考查了万有引力提供向心力和万有引力等于重力这两个理论,以及机械能守恒定律、能量守恒定律等,综合性较强,对学生的能力要求较高,需加强训练.

练习册系列答案
相关题目
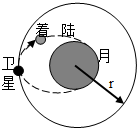 中国计划在2017年实现返回式月球软着陆器对月球进行科学探测,如图所示,届时发射一颗运动半径为r的绕月卫星,登月着陆器从绕月卫星出发,沿椭圆轨道降落到月球的表面上,与月球表面经多次碰撞和弹跳才停下来,假设着陆器第一次弹起的最大高度为h,水平速度为v1,第二次着陆时速度为v2,已知月球半径为R,着陆器质量为m,不计一切阻力和月球的自转.求:
中国计划在2017年实现返回式月球软着陆器对月球进行科学探测,如图所示,届时发射一颗运动半径为r的绕月卫星,登月着陆器从绕月卫星出发,沿椭圆轨道降落到月球的表面上,与月球表面经多次碰撞和弹跳才停下来,假设着陆器第一次弹起的最大高度为h,水平速度为v1,第二次着陆时速度为v2,已知月球半径为R,着陆器质量为m,不计一切阻力和月球的自转.求: