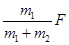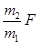题目内容
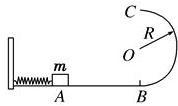
(16分)如图1所示,一质量为m的滑块(可视为质点)沿某斜面顶端A由静止滑下,已知滑块与斜面间的动摩擦因数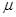 和滑块到斜面顶端的距离
和滑块到斜面顶端的距离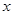 的关系如图2所示。斜面倾角为37°,长为L。有一半径
的关系如图2所示。斜面倾角为37°,长为L。有一半径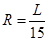 的光滑竖直半圆轨道刚好与斜面底端B相接,且直径BC与水平面垂直,假设滑块经过B点时没有能量损失。当滑块运动到斜面底端B又与质量为m的静止小球(可视为质点)发生弹性碰撞(已知:
的光滑竖直半圆轨道刚好与斜面底端B相接,且直径BC与水平面垂直,假设滑块经过B点时没有能量损失。当滑块运动到斜面底端B又与质量为m的静止小球(可视为质点)发生弹性碰撞(已知: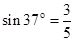 ,
,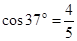 )。求:
)。求:
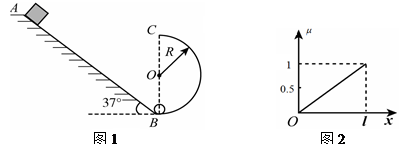
(1)滑块滑至斜面底端B时的速度大小;
(2)在B点小球与滑块碰撞后小球的速度大小;
(3)滑块滑至光滑竖直半圆轨道的最高点C时对轨道的压力。
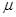 和滑块到斜面顶端的距离
和滑块到斜面顶端的距离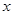 的关系如图2所示。斜面倾角为37°,长为L。有一半径
的关系如图2所示。斜面倾角为37°,长为L。有一半径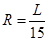 的光滑竖直半圆轨道刚好与斜面底端B相接,且直径BC与水平面垂直,假设滑块经过B点时没有能量损失。当滑块运动到斜面底端B又与质量为m的静止小球(可视为质点)发生弹性碰撞(已知:
的光滑竖直半圆轨道刚好与斜面底端B相接,且直径BC与水平面垂直,假设滑块经过B点时没有能量损失。当滑块运动到斜面底端B又与质量为m的静止小球(可视为质点)发生弹性碰撞(已知: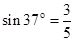 ,
,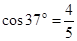 )。求:
)。求:
(1)滑块滑至斜面底端B时的速度大小;
(2)在B点小球与滑块碰撞后小球的速度大小;
(3)滑块滑至光滑竖直半圆轨道的最高点C时对轨道的压力。
(1)  (2)
(2) 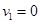 (3)
(3)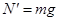
 (2)
(2) 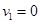 (3)
(3)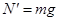
试题分析:(1)滑块由顶端滑至底端,由动能定理得:
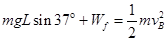 (2分)
(2分)由图2的物理意义得:
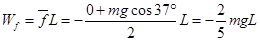 (2分)
(2分)解得
 (2分)
(2分)(2)滑块与小球发生弹性碰撞,设碰后速度分别为
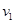 、
、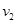 ,满足动量守恒和机械能守恒:
,满足动量守恒和机械能守恒: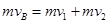 (2分)
(2分)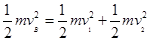 (2分)
(2分)解得:
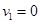 ,
,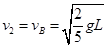 (1分)
(1分)说明:学生未列双守恒方程,直接利用速度交换的结论,只扣1分。
(3)滑块从B到C,由动能定理有:
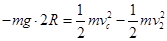 (2分)
(2分)解得:
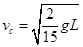
对滑块根据牛顿第二定律有:
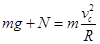 (2分)
(2分)解得:
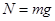
由牛顿第三定律得滑块在C点时对轨道的压力为
 (1分)
(1分)说明:学生未利用牛顿第三定律求压力,只扣1分

练习册系列答案
相关题目
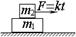

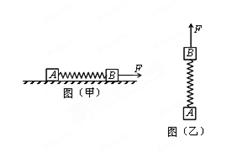
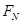 =_________,如果地面的动摩擦因数变小,两者一起沿水平地面作匀加速运动,则
=_________,如果地面的动摩擦因数变小,两者一起沿水平地面作匀加速运动,则