题目内容
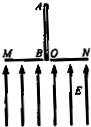 如图,MN为水平放置的金属板,板中央有一个小孔O,板下存在竖直向上的匀强电场.电场强度为E.AB是一根长为l,质量为m的均匀带正电的绝缘细杆.现将杆下端置于O处,然后将杆由静止释放,杆运动过程中始终保持竖直.当杆下落
如图,MN为水平放置的金属板,板中央有一个小孔O,板下存在竖直向上的匀强电场.电场强度为E.AB是一根长为l,质量为m的均匀带正电的绝缘细杆.现将杆下端置于O处,然后将杆由静止释放,杆运动过程中始终保持竖直.当杆下落| l | 3 |
(1)细杆带电荷量;
(2)杆下落的最大速度;
(3)若杆没有全部进入电场时速度减小为零,求此时杆下落的位移.
分析:下落
时速度最大,则加速度a=0,故重力和电场力平衡 mg=E
q,化简可得细杆带的电荷量.
从静止释放到下落
过程中,由动能定理:mg
-
×
=
mυm2-0,化简可得杆下落的最大速度.
从静止释放到下落到速度为零的过程中,由动能定理:mgh-
h=0-0,化简可得此时杆下落的位移.
| l |
| 3 |
| 1 |
| 3 |
从静止释放到下落
| l |
| 3 |
| l |
| 3 |
0+E
| ||
| 2 |
| l |
| 3 |
| 1 |
| 2 |
从静止释放到下落到速度为零的过程中,由动能定理:mgh-
0+E
| ||
| 2 |
解答:解:(1)由于下落
时速度最大,则加速度a=0
故重力和电场力平衡
所以有 mg=E
q
即 q=
(2)从静止释放到下落
过程中
由动能定理:mg
-
×
=
mυm2-0
所以 υm=
(3)设下落h时,速度为零
由动能定理:mgh-
h=0-0
所以 h=
答:(1)细杆带电荷量为
;(2)杆下落的最大速度为
;(3)此时杆下落的位移为
.
| l |
| 3 |
故重力和电场力平衡
所以有 mg=E
| 1 |
| 3 |
即 q=
| 3mg |
| E |
(2)从静止释放到下落
| l |
| 3 |
由动能定理:mg
| l |
| 3 |
0+E
| ||
| 2 |
| l |
| 3 |
| 1 |
| 2 |
所以 υm=
|
(3)设下落h时,速度为零
由动能定理:mgh-
0+E
| ||
| 2 |
所以 h=
| 2mgl |
| Eq |
答:(1)细杆带电荷量为
| 3mg |
| E |
|
| 2mgl |
| Eq |
点评:本题关键是要知道,杆子的电荷是均匀分布的,故杆子进入电场中库仑力是均匀增大的,其平均力可以
EQ表示,Q表示杆子在电场中部分的电荷量.
| 1 |
| 2 |

练习册系列答案
相关题目
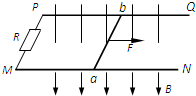 如图所示,水平放置的金属导轨MN、PQ处于竖直向下的匀强磁场中,导轨左端M、P连接电阻R,金属杆ab在水平力F的作用下沿导轨自静止开始向右运动,并与导轨接触良好.下列判断正确的是( )
如图所示,水平放置的金属导轨MN、PQ处于竖直向下的匀强磁场中,导轨左端M、P连接电阻R,金属杆ab在水平力F的作用下沿导轨自静止开始向右运动,并与导轨接触良好.下列判断正确的是( )| A、流过电阻R的电流方向为M→P | B、金属杆ab运动时相当于电源 | C、金属杆ab所受安培力方向向右 | D、穿过回路abPM的磁通量保持不变 |
 (2005?山东)如图,在一水平放置的平板MN的上方有匀强磁场,磁感应强度的大小为B,磁场方向垂直于纸面向里.许多质量为m带电量为+q的粒子,以相同的速率v沿位于纸面内的各个方向,由小孔O射人磁场区域.不计重力,不计粒子间的相互影响.下列图中阴影部分表示带电粒子能经过区域,其中R=mv/qB.哪个图是正确的?( )
(2005?山东)如图,在一水平放置的平板MN的上方有匀强磁场,磁感应强度的大小为B,磁场方向垂直于纸面向里.许多质量为m带电量为+q的粒子,以相同的速率v沿位于纸面内的各个方向,由小孔O射人磁场区域.不计重力,不计粒子间的相互影响.下列图中阴影部分表示带电粒子能经过区域,其中R=mv/qB.哪个图是正确的?( ) 如图所示,PQ和MN为水平放置的平行金属导轨,间距为l=1.0m,直流电源、电阻箱R串连接在两根导轨之间.导体棒ab跨放在导轨上,棒的质量为m=20g,棒的中点用细绳经轻滑轮与物体c相连,物体c的质量M=30g.在垂直导轨平面方向存在磁感应强度B=0.2T的匀强磁场,磁场方向竖直向上,重力加速g取10m/s2,导体棒与导轨间的最大静摩擦为f为导体棒ab重力的0.5倍,电源电动势E=10V,电源内阻、导轨的电阻、导体棒电阻均忽略不计,若要保持物体c静止不动,电阻箱R的阻值变化范围应为多大?流过棒的电流方向如何?
如图所示,PQ和MN为水平放置的平行金属导轨,间距为l=1.0m,直流电源、电阻箱R串连接在两根导轨之间.导体棒ab跨放在导轨上,棒的质量为m=20g,棒的中点用细绳经轻滑轮与物体c相连,物体c的质量M=30g.在垂直导轨平面方向存在磁感应强度B=0.2T的匀强磁场,磁场方向竖直向上,重力加速g取10m/s2,导体棒与导轨间的最大静摩擦为f为导体棒ab重力的0.5倍,电源电动势E=10V,电源内阻、导轨的电阻、导体棒电阻均忽略不计,若要保持物体c静止不动,电阻箱R的阻值变化范围应为多大?流过棒的电流方向如何?