题目内容
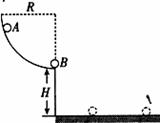
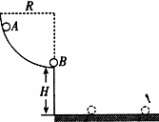
如图，固定于竖直平面内的四分之一光滑圆弧轨道半径为R，轨道底端距水平地面的高度为H．质量为mB的B球静止在圆弧轨道的底端，将质量为mA的A球从圆弧轨道上的某点由静止释放，它沿轨道滑下后与B球发生正碰．A、B两球落地时，水平通过的距离分别是s1和s2．已知重力加速度为g，不计空气阻力，且两球大小可忽略不计．求：
(1)B球被碰后落地的时间；
(2)A球释放的位置距圆弧轨道底端的高度h．
答案：
解析：
解析：
(12分)(1)B球被碰后做平抛运动，设落地时间为t，则
(3分)
(2)设A球释放的位置距圆轨道底端的高度为h，A与B相碰时的速度为v0，A、B相碰后的速度大小分别为vA、vB
对A球由机械能守恒得
(1分)
当mA＞mB时，由动量守恒得
(1分)
两球碰后做平抛运动，
(1分)
联立得
(3分)
当mA＜mB时，由动量守恒得
解得
(3分)
练习册系列答案
相关题目
如图所示，一高h=0.8m的光滑曲形槽底端B与水平传带平滑相接，传送带的运行速度为v0=6m/s，长为L=0.9m，滑块与传送带间的动摩擦因数μ=0.5，DEF为固定于竖直平面内的一段内壁光滑的中空方形细管，EF段被弯成以O为圆心、半径R=1.0m的一小段圆弧，管的D端弯成与水平传带C端平滑相接，O点位于地面，OF连线竖直．一质量为M=0.2kg的物块a从曲面槽顶端A点无初速释放，经B点滑到传送带上，过后滑块被传送带送入管DEF，管内顶端F点放置一质量为m=0.2kg的物块b，．已知a、b两物块均可视为质点，a、b横截面略小于管中空部分的横截面，重力加速度g取l0m/s2．求：
如图，一内壁光滑的环形细圆管，固定于竖直平面内，环的半径为R（比细管的直径大得多），在圆管中有一个直径与细管内径相同的小球（可视为质点），小球的质量为m，设某一时刻小球通过轨道的最低点时对管壁的压力为5.5mg．此后小球便作圆周运动，求：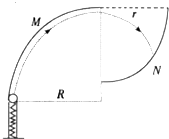
如图是为了检验某种防护罩承受冲击能力的装置，M为半径为R=1.0m、固定于竖直平面内的