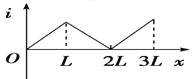
题目内容
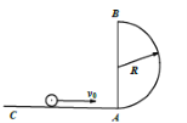
【题目】过山车是游乐场中常见的设施。图是一种过山车的简易模型,它由水平轨道和在竖直平面内的三个圆形轨道组成,B、C、D分别是三个圆形轨道的最低点,B、C间距与C、D间距相等,半径![]() =2.0 m、
=2.0 m、![]() =1.4 m。一个质量为m=1. 0 kg的小球(视为质点),从轨道的左侧A点以
=1.4 m。一个质量为m=1. 0 kg的小球(视为质点),从轨道的左侧A点以![]() =12.0m/s的初速度沿轨道向右运动,A、B间距
=12.0m/s的初速度沿轨道向右运动,A、B间距![]() ="6." 0 m。小球与水平轨道间的动摩擦因数
="6." 0 m。小球与水平轨道间的动摩擦因数![]() ="0." 2,圆形轨道是光滑的。假设水平轨道足够长,圆形轨道间不相互重叠。重力加速度取
="0." 2,圆形轨道是光滑的。假设水平轨道足够长,圆形轨道间不相互重叠。重力加速度取![]() ,计算结果保留小数点后一位数字。试求
,计算结果保留小数点后一位数字。试求
(1)小球在经过第一个圆形轨道的最高点时,轨道对小球作用力的大小;
(2)如果小球恰能通过第二个圆形轨道,B、C间距L应是多少;
(3)在满足(2)的条件下,如果要使小球不脱离轨道,在第三个圆形轨道的设计中,半径![]() 应满足的条件;小球最终停留点与起点A的距离。
应满足的条件;小球最终停留点与起点A的距离。
【答案】F="10.0" NL="12.5" m![]() 26.0 m。
26.0 m。
【解析】
试题(1)(4分)设小于经过第一个圆轨道的最高点时的速度为v1根据动能定理
![]() ①
①
小球在最高点受到重力mg和轨道对它的作用力F,根据牛顿第二定律
![]() ②
②
由①②得![]() ③
③
(2)(4分)设小球在第二个圆轨道的最高点的速度为v2,由题意
![]() ④
④
![]() ⑤
⑤
由④⑤得![]() ⑥
⑥
(3)(4分)要保证小球不脱离轨道,可分两种情况进行讨论:
I.轨道半径较小时,小球恰能通过第三个圆轨道,设在最高点的速度为v3,应满足
![]() ⑦
⑦
![]() ⑧
⑧
由⑥⑦⑧得![]()
II.轨道半径较大时,小球上升的最大高度为R3,根据动能定理
![]()
解得![]()
为了保证圆轨道不重叠,R3最大值应满足
![]()
解得 R3=27.9m
综合I、II,要使小球不脱离轨道,则第三个圆轨道的半径须满足下面的条件
![]()
或![]()
当![]() 时,小球最终焦停留点与起始点A的距离为L′,则
时,小球最终焦停留点与起始点A的距离为L′,则
![]()
![]()
当![]() 时,小球最终焦停留点与起始点A的距离为L〞,则
时,小球最终焦停留点与起始点A的距离为L〞,则
![]()