��Ŀ����
 ��1����ԭ�ӵ�n�ܼ�������ΪEn=
��1����ԭ�ӵ�n�ܼ�������ΪEn=| E1 |
| n2 |
| 3 |
| 16 |
| 3 |
| 4 |
��2����ͼ��ʾ����ֱƽ��ֱ��Ϊ��ǿ�糡�ĵ糡�ߣ��糡����δ֪��A��B�ǵ糡�е����㣬AB��������߳�Ϊl����糡�����е����Ϊ�ȣ�һ������Ϊm�������Ϊ-q�Ĵ��������Գ��ٶ�v0��A�㴹ֱ����糡���ô�������ǡ���ܾ���B�㣮�����Ǵ������ӵ�������С��
������ѧ��������ѧ���ɺ�������������Ϣ���Է�ӳ�糡�������ʵ�������������糡ǿ�ȣ�������������Щ�����жϺ������Щ���������
��������1�������ܼ���ԾǨ����Ĺ��������������ܼ�����ܼ���Լ����ڼ���̬�������ͻ�̬�����Ĺ�ϵ�����ԭ�ӷ������ǰ��ֱ��ڵ��ܼ���
��2�������ڵ糡������ƽ���˶�����ϴ���������ˮƽ�������ֱ�����ϵ��˶��������AB����ĵ糡ǿ�ȣ��Լ�������ǿ�糡�ĵ��Ʋ�Ĺ�ʽ���A��B����ĵ��Ʋͨ�����ӵĵ����жϵ糡ǿ�ȵķ��Ӷ�ȷ��A��B������Ƶĸߵͣ�
��2�������ڵ糡������ƽ���˶�����ϴ���������ˮƽ�������ֱ�����ϵ��˶��������AB����ĵ糡ǿ�ȣ��Լ�������ǿ�糡�ĵ��Ʋ�Ĺ�ʽ���A��B����ĵ��Ʋͨ�����ӵĵ����жϵ糡ǿ�ȵķ��Ӷ�ȷ��A��B������Ƶĸߵͣ�
����⣺��1������ԭ�ӷ������ǰ��ֱ�λ�ڵ�l���m�ܼ����������У�
-
=-
E1
-E1=-
E1
��ã�m=2
l=4
����ԭ�ӷ������ǰ��ֱ��ڵ�4�ܼ��͵�2�ܼ���
��2�������Ӵ�����������ƫת���ʵ糡���������£����Ե糡������ֱ���ϣ�
ˮƽ���������˶����У�lsin��=v0t
��ֱ���������ٶ�Ϊ����ȼ����˶�����lcos��=
at2
����ٶȣ�a=
��qE=ma���õ糡ǿ�ȴ�С��E=
=
B��ĵ��Ƹ���A��ĵ��ƣ���A��B�����ĵ��Ʋ�Ϊ��
UAB=-Elcos��=-
=-
cot2��
��B��ĵ��Ƹ���A��ĵ��ƣ���A��B�����ĵ��Ʋ�Ϊ-
cot2����
| E1 |
| l2 |
| E1 |
| m2 |
| 3 |
| 16 |
| E1 |
| m2 |
| 3 |
| 4 |
��ã�m=2
l=4
����ԭ�ӷ������ǰ��ֱ��ڵ�4�ܼ��͵�2�ܼ���
��2�������Ӵ�����������ƫת���ʵ糡���������£����Ե糡������ֱ���ϣ�
ˮƽ���������˶����У�lsin��=v0t
��ֱ���������ٶ�Ϊ����ȼ����˶�����lcos��=
| 1 |
| 2 |
����ٶȣ�a=
2
| ||
| lsin2�� |
��qE=ma���õ糡ǿ�ȴ�С��E=
| ma |
| q |
2m
| ||
| qlsin2�� |
B��ĵ��Ƹ���A��ĵ��ƣ���A��B�����ĵ��Ʋ�Ϊ��
UAB=-Elcos��=-
2m
| ||
| qsin2�� |
2m
| ||
| q |
��B��ĵ��Ƹ���A��ĵ��ƣ���A��B�����ĵ��Ʋ�Ϊ-
2m
| ||
| q |
���������⿼�����ܼ���ԾǨ�Լ����������ڵ糡�е��˶����ڶ����ǵ������⣬�ؼ�ץס���ӵ��˶����ɽ�����⣮

��ϰ��ϵ�д�
�����Ŀ
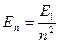 ��������1�ǻ�̬��������n=1��2��������һ��ԭ�ӷ�������Ϊ
��������1�ǻ�̬��������n=1��2��������һ��ԭ�ӷ�������Ϊ �Ĺ��Ӻ��ڱȻ�̬�����߳�
�Ĺ��Ӻ��ڱȻ�̬�����߳� �ļ���̬������ԭ�ӷ������ǰ��ֱ��ڵڼ��ܼ���
�ļ���̬������ԭ�ӷ������ǰ��ֱ��ڵڼ��ܼ���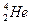 ����ͬ�����˶����ʺˣ�
����ͬ�����˶����ʺˣ�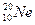 �������������������������ǡ�þ�ֹ������ײǰ���ʺ˵��ٶȣ������������������
�������������������������ǡ�þ�ֹ������ײǰ���ʺ˵��ٶȣ������������������
 ����
���� �ǻ�̬��������n=1��2��������һ��ԭ�ӷ�������Ϊ
�ǻ�̬��������n=1��2��������һ��ԭ�ӷ�������Ϊ �Ĺ��Ӻ��ڱȻ�̬�����߳�
�Ĺ��Ӻ��ڱȻ�̬�����߳� �ļ���̬������ԭ�ӷ������ǰ��ֱ��ڵڼ��ܼ���
�ļ���̬������ԭ�ӷ������ǰ��ֱ��ڵڼ��ܼ��� ����ͬ�����˶����ʺˣ�
����ͬ�����˶����ʺˣ� �������������������������ǡ�þ�ֹ������ײǰ���ʺ˵��ٶȣ������������������
�������������������������ǡ�þ�ֹ������ײǰ���ʺ˵��ٶȣ������������������