题目内容
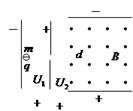
(10分)如图所示,平行金属极板A、B水平放置,A板带正电,B板带负电,两板间的电压为U,距离为2d,一个半径为d的绝缘光滑半圆形轨道,竖直放置在两极板中,轨道最高点和圆心O的连线与极板平行.在轨道最高点边缘处有一质量为m,电量为+ q的小球,由静止开始下滑。重力加速度为g。
求:(1)轨道最高点与最低点间的电势差;(2)小球到达最低点时的速度大小;(3)小球经过最低点时对轨道压力的大小。

求:(1)轨道最高点与最低点间的电势差;(2)小球到达最低点时的速度大小;(3)小球经过最低点时对轨道压力的大小。

(1)U/2 (2)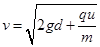 (3)
(3)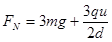
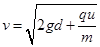 (3)
(3)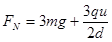
试题分析:(1)由于是匀强电场,则

∴最高点与最低点电势差
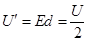
(2)从最高点到最低点,由动能定理可得:
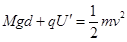
∴
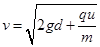
(3)在最低点有:
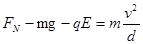
∴
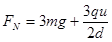
由牛顿第三定律可知:球对轨道压力大小
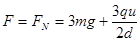
点评:此类题型属于较常见的匀强电场问题,设计的问题也多为常见题型,涉及到动能定理的运用,以及在最低点圆周运动的向心力的表达

练习册系列答案
相关题目
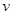 (未知)射出,侧移量为y,不计粒子的重力,则下列说法中正确的是
(未知)射出,侧移量为y,不计粒子的重力,则下列说法中正确的是 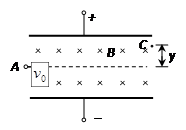
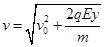
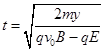
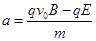 ,方向时刻改变
,方向时刻改变
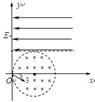
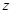 轴正方向进入匀强电场
轴正方向进入匀强电场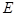 和匀强磁场
和匀强磁场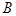 ,经偏转后打在荧光屏上
,经偏转后打在荧光屏上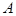 点处,则( )
点处,则( )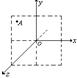
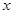 轴正方向
轴正方向 轴正方向
轴正方向