题目内容
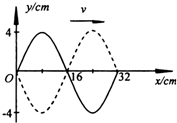 沿x轴正方向传播的一列横波在t=0时刻的波形如图所示,在t=0.1s时刻波形如虚线所知此波的周期大于0.1s,O点不是振源.求:
沿x轴正方向传播的一列横波在t=0时刻的波形如图所示,在t=0.1s时刻波形如虚线所知此波的周期大于0.1s,O点不是振源.求:(1)此波的波速;
(2)x轴上坐标x=16cm的质点在波谷的时刻;
(3)距坐标x=12cm的质点最近的与它位移始终相同的点的x坐标;
(4)此波进入另一介质中波速变为3.2m/s,它在这一介质中的波长是多少?
分析:(1)根据波的周期性,定出时间与周期的关系式,结合条件,求出周期,读出波长,即可求得波速.
(2)简谐波沿x轴正方向传播,由波形平移法判断出x=16cm质点的振动方向,由周期性写出x=16cm的质点在波谷的时刻表达式.
(3)位移总是相等的质点间距离为波长的整数倍,离x=12 cm的质点最近与它位移相同的点与它相距一个波长,即可写出其坐标.
(4)波进入另一介质中时频率不变,由波速公式v=λf求解.
(2)简谐波沿x轴正方向传播,由波形平移法判断出x=16cm质点的振动方向,由周期性写出x=16cm的质点在波谷的时刻表达式.
(3)位移总是相等的质点间距离为波长的整数倍,离x=12 cm的质点最近与它位移相同的点与它相距一个波长,即可写出其坐标.
(4)波进入另一介质中时频率不变,由波速公式v=λf求解.
解答:解:(1)由图中可得λ=0.32 m,波形由实线变成虚线所用的时间
△t=(n+
)T(n=0,1,2,3…)
由于T>△t,n只能取0,所以T=0.2 s
v=
=
=1.6 m/s
(2)t=0时,x=16 cm的质点的振动方向向上,则在波谷时刻
t=(n+
)T=(n+
)×0.2=0.2 n+0.15(s)(n=0,1,2,3…)
(3)位移总是相等的质点间距离为波长的整数倍,因此离x=12 cm的质点最近与它位移相同的点与它相距一个波长,其坐标有两个.
x1=12 cm+32 cm=44 cm
x2=12 cm-32 cm=-20 cm
(4)波进入另一介质时,频率f不变,由v=λf得λ′=
λ=0.64 m
答:
(1)此波的波速是1.6m/s;
(2)x轴上坐标x=16cm的质点在波谷的时刻是t=0.2 n+0.15(s)(n=0,1,2,3…);
(3)距坐标x=12cm的质点最近的与它位移始终相同的点的x坐标是44cm和-20cm;
(4)此波进入另一介质中波速变为3.2m/s,它在这一介质中的波长是0.64m.
△t=(n+
| 1 |
| 2 |
由于T>△t,n只能取0,所以T=0.2 s
v=
| λ |
| T |
| 0.32 |
| 0.2 |
(2)t=0时,x=16 cm的质点的振动方向向上,则在波谷时刻
t=(n+
| 3 |
| 4 |
| 3 |
| 4 |
(3)位移总是相等的质点间距离为波长的整数倍,因此离x=12 cm的质点最近与它位移相同的点与它相距一个波长,其坐标有两个.
x1=12 cm+32 cm=44 cm
x2=12 cm-32 cm=-20 cm
(4)波进入另一介质时,频率f不变,由v=λf得λ′=
| v′ |
| v |
答:
(1)此波的波速是1.6m/s;
(2)x轴上坐标x=16cm的质点在波谷的时刻是t=0.2 n+0.15(s)(n=0,1,2,3…);
(3)距坐标x=12cm的质点最近的与它位移始终相同的点的x坐标是44cm和-20cm;
(4)此波进入另一介质中波速变为3.2m/s,它在这一介质中的波长是0.64m.
点评:本题是多解问题,关键要理解波空间的周期性和时间的周期性,不能漏解.

练习册系列答案
相关题目
 (2005?烟台模拟)如图所示,沿x轴正方向传播的一列简谐波在某时刻的波形图为一正弦曲线,其波速为200m/s,则可推出,其中正确的( )
(2005?烟台模拟)如图所示,沿x轴正方向传播的一列简谐波在某时刻的波形图为一正弦曲线,其波速为200m/s,则可推出,其中正确的( ) (2013?南宁三模)如图所示,沿x轴正方向传播的一列简谐横波在某时刻的波形图为一正弦曲线,其波速为200m/s,下列说法中正确的是( )
(2013?南宁三模)如图所示,沿x轴正方向传播的一列简谐横波在某时刻的波形图为一正弦曲线,其波速为200m/s,下列说法中正确的是( )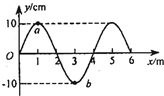 如图是沿x轴正方向传播的一列简谐横波在某时刻的图象,已知该波的波速为20m/s,则( )
如图是沿x轴正方向传播的一列简谐横波在某时刻的图象,已知该波的波速为20m/s,则( )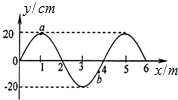 沿x轴正方向传播的一列简谐横波在t=0时刻的波形曲线如图所示,其波速为10m/s,该时刻波恰好传播到x=6m的位置.介质中有a、b两质点,下列说法中正确的是( )
沿x轴正方向传播的一列简谐横波在t=0时刻的波形曲线如图所示,其波速为10m/s,该时刻波恰好传播到x=6m的位置.介质中有a、b两质点,下列说法中正确的是( )