题目内容
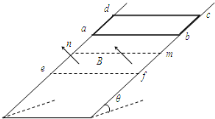
【题目】如图所示，电阻不计的轨道MON和PO′Q平行放置，两轨道的间距L=1m，ON及O′Q与水平面的夹角θ=53°，整个空间存在竖直向上的匀强磁场，磁感应强度B=1T。现将两根相同的金属棒ab和cd分别置于导轨上并与导轨垂直且始终保持良好接触，两棒与OO′相距足够远。已知每根棒的质量m=1.0kg、电阻R=0.5Ω，棒与导轨间动摩擦因数μ=0.5，g取10m/s2。(sin53°=0.8，cos53°=0.6)
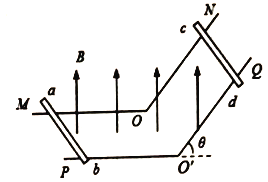
(1)使ab棒以v1=5m/s向左匀速运动，求释放cd棒瞬间，cd棒受到安培力的大小和方向，并分析cd棒以后的运动情况；
(2)保持ab棒以恒定速度v匀速运动，释放cd棒，稳定后cd棒以v2=10m/s的速度沿斜面匀速运动，求ab棒的速度v大小和方向。
【答案】(1)5N 方向水平向左 cd棒做加速度减小的加速运动，最终匀速 (2)61m/s 方向向右
【解析】
（1）释放cd棒瞬间，计算出回路的电动势和感应电流，由安培力F=BIL可得安培力大小，由左手定则确定安培力的方向。cd棒在释放以后的时间里，随着cd棒运动的加快，回路中出现了反电动势，最终安培力向右到达平衡，cd棒做匀速运动。
（2）由于cd棒在斜轨上是匀速运动，由平衡条件可知，cd棒受到的安培力水平向右，考虑两种情况：cd棒沿轨道向上和cd棒沿轨道向下运动，分别根据平衡知识得安培力的表达式，然后由闭合电路欧姆定律求出电流，由F安=BIL求出安培力，进行求解即可。
（1）刚释放cd棒时，电路中的电动势E=BLv1=5V，感应电流I=
=5A，cd棒受到的安培力：F安=BIL=5N，方向水平向左。释放cd棒后，随着cd棒运动的加快，回路中出现了反电动势，cd棒在运动过程中受到的安培力先向左后向右，由于摩擦力和安培力的共同影响，做加速度逐渐减小的加速运动，最终做匀速运动。
（2）由于cd棒在斜轨上是匀速运动，由平衡条件可知，cd棒受到的安培力水平向右，设cd棒沿轨道向上运动受到的安培力为F安1，则有：
F安1
=mg
+
N
N=mg+F安
得F安1=
=55N，此时ab棒应向右运动
电路中的电动势E=BLv-BLv2
I=
F安1=
解得ab棒的速度：v=61m/s,方向向右。
设cd棒沿轨道向下运动受到的安培力为F安2，则有：
F安2+N=mg
N=mg+F安2
解得：F安2=
=5N，设ab棒向右运动，电路中的电动势：E=BLv+BLv2
F安2=
解得：v=-1m/s，“-”号表示ab棒向左运动，与题设ab棒向右运动相矛盾，即这种情况不可能。
所以ab棒的速度为v=61m/s，方向向右。
