题目内容
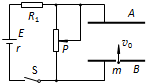 在如图所示的电路中,两平行正对金属板A、B水平放置,两板间的距离d=4.0cm.电源电动势E=400V,内电阻r=20Ω,电阻R1=1980Ω.闭合开关S,待电路稳定后,将一带正电的小球(可视为质点)从B板上的小孔以初速度v0=1.0m/s竖直向上射入两板间,小球恰好能到达A板.若小球所带电荷量q=1.0×10-7C,质量m=2.0×10-4kg,不考虑空气阻力,忽略射入小球对电路的影响,取g=10m/s2.求:
在如图所示的电路中,两平行正对金属板A、B水平放置,两板间的距离d=4.0cm.电源电动势E=400V,内电阻r=20Ω,电阻R1=1980Ω.闭合开关S,待电路稳定后,将一带正电的小球(可视为质点)从B板上的小孔以初速度v0=1.0m/s竖直向上射入两板间,小球恰好能到达A板.若小球所带电荷量q=1.0×10-7C,质量m=2.0×10-4kg,不考虑空气阻力,忽略射入小球对电路的影响,取g=10m/s2.求:(1)A、B两金属板间的电压的大小U;
(2)滑动变阻器消耗的电功率P滑;
(3)电源的效率η.
分析:(1)小球从B板上的小孔射入恰好到达A板的过程中,在电场力和重力的作用下做匀减速直线运动,电场力做功-qU,重力做功-mgd,根据动能定理求解U.
(2)变阻器两端的电压等于U,由I=
,U=IR滑,相结合求出R滑,滑动变阻器消耗的电功率 P滑=
.
(3)电源的效率η=
=
.
(2)变阻器两端的电压等于U,由I=
| E |
| R1+R滑+r |
| U2 |
| R滑 |
(3)电源的效率η=
| P出 |
| P总 |
| I2(R1+R滑) |
| I2(R1+R滑+r) |
解答:解:(1)小球从B板上的小孔射入恰好到达A板的过程中,在电场力和重力的作用下做匀减速直线运动,设A、B两极板间电压为U,根据动能定理有
-qU-mgd=0-
mv02
解得U=200V
(2)设此时滑动变阻器接入电路中的电阻值为R滑,根据闭合电 路欧姆定律可知,电路中的电流
得 I=
根据部分电路欧姆定律可知 U=IR滑
解得 R滑=2.0×103Ω
滑动变阻器消耗的电功率 P滑=
=20W
(3)电源的效率η=
×100%=
×100%=99.5%.
答:
(1)A、B两金属板间的电压的大小U是200V;
(2)滑动变阻器消耗的电功率P滑是2.0×103Ω.
(3)电源的效率η是99.5%.
-qU-mgd=0-
| 1 |
| 2 |
解得U=200V
(2)设此时滑动变阻器接入电路中的电阻值为R滑,根据闭合电 路欧姆定律可知,电路中的电流
得 I=
| E |
| R1+R滑+r |
根据部分电路欧姆定律可知 U=IR滑
解得 R滑=2.0×103Ω
滑动变阻器消耗的电功率 P滑=
| U2 |
| R滑 |
(3)电源的效率η=
| P出 |
| P总 |
| I2(R1+R滑) |
| I2(R1+R滑+r) |
答:
(1)A、B两金属板间的电压的大小U是200V;
(2)滑动变阻器消耗的电功率P滑是2.0×103Ω.
(3)电源的效率η是99.5%.
点评:本题电场与电路的综合应用,小球在电场中做匀减速运动,由动能定理求电压.根据电路的结构,由欧姆定律求变阻器接入电路的电阻.难度不大.

练习册系列答案
相关题目
 标有“8V 6.4W”和“8V 20W”字样的L1、L2两只灯泡连接在如图所示的电路中,C点接地.如果将电路中L1、L2两灯的位置互换,则( )
标有“8V 6.4W”和“8V 20W”字样的L1、L2两只灯泡连接在如图所示的电路中,C点接地.如果将电路中L1、L2两灯的位置互换,则( ) (2009?天津模拟)在如图所示的电路中,灯泡L的电阻大于电源的内阻r,闭合电键S,将滑动变阻器滑片P向左移动一段距离后,下列结论正确的是( )
(2009?天津模拟)在如图所示的电路中,灯泡L的电阻大于电源的内阻r,闭合电键S,将滑动变阻器滑片P向左移动一段距离后,下列结论正确的是( ) 在如图所示的电路中,R3=4Ω,A的示数为0.75A,V的示数为2V.突然有一个电阻被烧断,使得A的示数变为0.80A,V的示数变为3.2V(图中电表均视为理想电表).?
在如图所示的电路中,R3=4Ω,A的示数为0.75A,V的示数为2V.突然有一个电阻被烧断,使得A的示数变为0.80A,V的示数变为3.2V(图中电表均视为理想电表).? (2012?西城区模拟)在如图所示的电路中,电源的电动势E=1.5V,内电阻r=1.0Ω,电阻R=4.0Ω,不计电流表的内阻.闭合开关S后,电流表的示数为( )
(2012?西城区模拟)在如图所示的电路中,电源的电动势E=1.5V,内电阻r=1.0Ω,电阻R=4.0Ω,不计电流表的内阻.闭合开关S后,电流表的示数为( )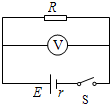 在如图所示的电路中,已知电源的电动势E=1.5V,内电阻r=1.0Ω,电阻R=2.0Ω.闭合开关S后,电阻R两端的电压U等于( )
在如图所示的电路中,已知电源的电动势E=1.5V,内电阻r=1.0Ω,电阻R=2.0Ω.闭合开关S后,电阻R两端的电压U等于( )