Question

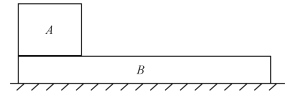
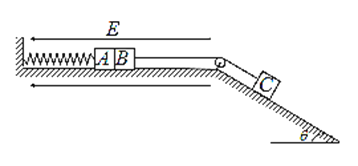
【题目】如图所示，在绝缘水平面上的两物块A、B贴放在一起，劲度系数为k的水平绝缘轻质弹簧一端与固定的墙壁相连，另一端与A物体连接，物块B、C用跨过定滑轮的绝缘轻绳连接，C在倾角为θ=的长斜面上，滑轮两侧的轻绳分别与水平面和斜面平行。A、B、C的质量分别是m、2m、4m，A、C均不带电，B带正电，电量为q，滑轮左侧存在着水平向左的匀强电场，场强整个系统不计一切摩擦，B与滑轮足够远。开始时用手托住C，使A、B静止且轻绳刚好伸直。然后放开手，让C开始下滑，直到A、B分离，弹簧始终未超过弹性限度，重力加速度大小为g。求：

（1）系统静止时弹簧的压缩长度x1；

（2）从C开始下滑到A、B刚要分离的过程中B的电势能的改变量 ；

（3）若从C开始下滑，至到A、B分离，弹簧弹性势能减少了EP，求A、B分离时B物体的速度大小v。

Answer 1

【答案】(1)(2)(3)

【解析】

(1)系统静止时，对A物体

解得：

(2)A、B分离时，A、B间的弹力为零，A、B、C具有相同的加速度a，设此时轻绳的拉力为T，弹簧压缩量为，对B：

对C：

对A：

B物体电势能的增加量：

解得：

即B的电势能增加了

(3)对A、B、C和弹簧组成的系统，根据能量守恒定律

解得