Question

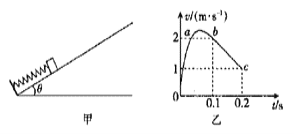
【题目】如图甲所示，足够长的固定粗糙斜面的倾角θ=30°，斜面的底端有一挡板，与斜面平行的轻质弹簧的一端固定在挡板上，质量m=0. 5kg的滑块（可视为质点）压缩弹簧，滑块与弹簧不拴接。现将滑块由静止释放，从释放滑块开始计时，计算机通过传感器描绘出滑块在0~0.2s内的（图像如图乙所示，其中Oab段为曲线，bc段为直线。已知滑块由静止释放时弹簧的弹性势能Ep= 2J，取g = 10 m/ s2，求：

(1)0~0.1s滑块与斜面间的动摩擦因数；

(2)0~0.1s内滑块沿斜面上滑的距离。

Answer 1

【答案】（1）；（2）0.2m

【解析】

(1)由题图乙可知，0.1 s~0. 2 s内滑块离开弹簧沿斜面向上做匀减速直线运动，加速度的大小为

由牛顿第二定律有

解得。

(2)由题图乙可知，t1=0.1 s时滑块的速度大小为v=2 m/s， 0~0.1 s内，由功能关系有

解得x=0.2 m。

答：(1)0~0.1s滑块与斜面间的动摩擦因数；

(2)0~0.1s内滑块沿斜面上滑的距离x=0.2 m。