题目内容
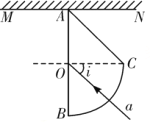
【题目】如图示,质量为m1的小球A用不可伸长的轻质细绳悬挂,从偏离竖直方向θ角位置静止释放,在最低点与静止小球B发生对心弹性碰撞, B球位于四分之一圆弧CD的圆心O处的光滑小支架上,圆弧半径与细绳长度均为R,OC边水平,B球质量为m2,A、B小球可视为质点,求
(1)A球摆到最低点与B球发生碰撞前绳子的拉力大小F;
(2)碰后B球的速度大小vB;
(3)小球B到达圆弧面的最小动能EK

【答案】⑴![]() ⑵
⑵![]() ⑶
⑶![]()
【解析】试题分析:根据机械能守恒求出速度,再根据牛顿第二定律求出拉力;碰撞过程中满足动量守恒和机械能守恒,即可求出碰后的速度;小球碰后做圆周运动,根据平抛公式再结合动能定理求出最小的动能。
⑴小球A下降过程机械能守恒: ![]()
最低点由牛顿第二定律有: ![]()
联立解得: ![]()
(2)小球A下降过程机械能守恒: ![]()
解得: ![]()
AB发生弹性碰撞瞬间:
动量守恒: ![]()
机械能守恒: ![]()
联立解得: ![]()
(3)碰后小球平抛至圆弧时,设竖直位移为y,水平位移为x
则 : ![]()
水平方向匀速: ![]()
竖直方向自由落体: ![]()
由以上联立解得: 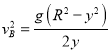
又由平抛过程机械能守恒有: ![]()
联立以上解得: 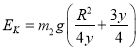
由数学知识可知当: ![]()
动能具有最小值,最小值为: ![]()

练习册系列答案
相关题目