题目内容
11.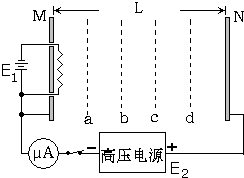 当金属的温度升高到一定程度时就会向四周发射电子,这种电子叫热电子.通常情况下,热电子的初速度可以忽略不计.如图,相距为L的两平行金属板之间接上高压电源E2,E2的电压恒定为U.电源E1是用来给灯丝加热而产生热电子的,灯丝与M板靠得很近(M、N之间可当作匀强电场).a、b、c、d是匀强电场中的四个均匀分布的等势面.当电源接通后,电流表的示数为I,且保持不变.已知热电子的质量是m、电量是e.求:
当金属的温度升高到一定程度时就会向四周发射电子,这种电子叫热电子.通常情况下,热电子的初速度可以忽略不计.如图,相距为L的两平行金属板之间接上高压电源E2,E2的电压恒定为U.电源E1是用来给灯丝加热而产生热电子的,灯丝与M板靠得很近(M、N之间可当作匀强电场).a、b、c、d是匀强电场中的四个均匀分布的等势面.当电源接通后,电流表的示数为I,且保持不变.已知热电子的质量是m、电量是e.求:(1)电子经过等势面c时的速度是多大?
(2)c、d两等势面之间的电子数N1是多少?
(3)d、N两等势面之间的电子数N2与c、d两等势面之间的电子数N1的比值是多少?
分析 (1)根据U=Ed求解电场强度,对M到C过程根据动能定理列式求解即可;
(2)对M到d过程根据动能定理列式d位置速度;然后根据平均速度公式求解从c到d的时间,最后根据q=It=Ne求解电子数目;
(3)与第二问同样方法先求解d、N两等势面之间的电子数N2,然后即可得到比值.
解答 解:(1)电子M→c过程:
E=$\frac{U}{L}$,
${U}_{MC}=-E•\frac{3}{5}L=-\frac{3}{5}U$,
根据动能定理,有:
${U}_{MC}(-e)=\frac{1}{2}m{v}_{C}^{2}-0$
联立解得:
${v}_{C}=\sqrt{\frac{6Ue}{5m}}$
(2)电阻M→d过程:
E=$\frac{U}{L}$,
${U}_{MC}=-E•\frac{4}{5}L=-\frac{4}{5}U$,
根据动能定理,有:
${U}_{Md}(-e)=\frac{1}{2}m{v}_{d}^{2}-0$
联立解得:
${v}_{d}=\sqrt{\frac{8Ue}{5m}}$,
从c到d过程,有:
${t}_{cd}=\frac{\frac{L}{5}}{{\overline{v}}_{cd}}$=$\frac{\frac{L}{5}}{\frac{{v}_{c}+{v}_{d}}{2}}$=$\frac{\frac{2L}{5}}{\sqrt{\frac{6Ue}{5m}}+\sqrt{\frac{8Ue}{5m}}}$=L$\sqrt{\frac{2m}{5Ue}}(\sqrt{4}-\sqrt{3})$
${N}_{1}={N}_{cd}=\frac{I•{t}_{cd}}{e}=\frac{IL}{e}\sqrt{\frac{2m}{5Ue}}(\sqrt{4}-\sqrt{3})$
(3)由M→N过程,根据动能定理,有:
$-U(-e)=\frac{1}{2}m{v}_{N}^{2}-0$,
解得:${v}_{N}=\sqrt{\frac{2Ue}{m}}$,
${t}_{dN}=\frac{\frac{L}{5}}{{\overline{v}}_{dN}}=\frac{\frac{L}{5}}{\frac{{v}_{N}+{v}_{d}}{2}}=\frac{\frac{2L}{5}}{\sqrt{\frac{2Ue}{m}}+\sqrt{\frac{8Ue}{5m}}}$=L$\sqrt{\frac{2m}{5Ue}}(\sqrt{5}-\sqrt{4})$
${N}_{2}={N}_{dN}=\frac{I•{t}_{dN}}{e}=\frac{IL}{e}\sqrt{\frac{2m}{5Ue}}(\sqrt{5}-\sqrt{4})$
故$\frac{{N}_{1}}{{N}_{2}}=\frac{\sqrt{4}-\sqrt{3}}{\sqrt{5}-\sqrt{4}}=\frac{2-\sqrt{3}}{\sqrt{5}-2}$
答:(1)电子经过等势面c时的速度是$\sqrt{\frac{6Ue}{5m}}$;
(2)c、d两等势面之间的电子数N1是$\frac{IL}{e}\sqrt{\frac{2m}{5Ue}}(\sqrt{4}-\sqrt{3})$;
(3)d、N两等势面之间的电子数N2是$\frac{IL}{e}\sqrt{\frac{2m}{5Ue}}(\sqrt{5}-\sqrt{4})$,
与c、d两等势面之间的电子数N1的比值是$\frac{2-\sqrt{3}}{\sqrt{5}-2}$.
点评 本题考查了动能定理、牛顿第二定律和运动学公式的综合运用,关键要正确建立物理模型,依据相关物理规律求解.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 温度是物体内能大小的标志 | |
| B. | 直接来处自然界的能源叫一次能源 | |
| C. | 能源被使用过程中总能量虽然守恒,但能量的可利用价值会降低 | |
| D. | 太阳能、石油、天然气、地热能、核能都属于新能源 |
| A. | 10N/m | B. | 100 N/m | C. | 200 N/m | D. | 400 N/m |
 如图所示,A、B是某电场中一条电场线上的两点.一个带负电的点电荷仅受电场力作用,从A点沿电场线运动到B点过程中,其速度v随时间t变化的规律如图乙所示.则下列说法中正确的是( )
如图所示,A、B是某电场中一条电场线上的两点.一个带负电的点电荷仅受电场力作用,从A点沿电场线运动到B点过程中,其速度v随时间t变化的规律如图乙所示.则下列说法中正确的是( )| A. | A点的电场强度比B点的大 | B. | A、B两点的电场强度相等 | ||
| C. | 电场线方向由A指向B | D. | 电场线方向由B指向A |
| A. | 它们运动的轨道半径之比为8:1 | B. | 它们运动的轨道半径之比为4:1 | ||
| C. | 它们运动的向心加速度之比为1:8 | D. | 它们运动的向心力之比为1:32 |
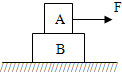 如图所示,重力都是G的A、B两个物体叠放在一起,现用力F水平向右拉A,若两个物体仍保持静止状态,则可知:A受4个力;B受4个力.
如图所示,重力都是G的A、B两个物体叠放在一起,现用力F水平向右拉A,若两个物体仍保持静止状态,则可知:A受4个力;B受4个力. 如图所示,带电量为+q的点电荷与均匀带电为Q的薄板相距为2L,点电荷到带电薄板的垂线通过板的几何中心.若图中a点处的电场强度为零,根据对称性,图中b点处产生的电场强度大小为$\frac{10kq}{9{L}^{2}}$,方向水平向右.(静电力恒量为k)
如图所示,带电量为+q的点电荷与均匀带电为Q的薄板相距为2L,点电荷到带电薄板的垂线通过板的几何中心.若图中a点处的电场强度为零,根据对称性,图中b点处产生的电场强度大小为$\frac{10kq}{9{L}^{2}}$,方向水平向右.(静电力恒量为k) 如图所示,一物体的质量m=2kg,在倾角θ=30°的光滑斜面上的A点由静止下滑,A点距弹簧上端B的距离AB=2.5m,当物体到达B后将弹簧压缩到最低点C,BC=1.62m,挡板及弹簧的质量不计,弹簧的劲度系数为100N/m,弹簧的g取10m/s2,sin37°=0.6.求:
如图所示,一物体的质量m=2kg,在倾角θ=30°的光滑斜面上的A点由静止下滑,A点距弹簧上端B的距离AB=2.5m,当物体到达B后将弹簧压缩到最低点C,BC=1.62m,挡板及弹簧的质量不计,弹簧的劲度系数为100N/m,弹簧的g取10m/s2,sin37°=0.6.求: