题目内容
 今年2月28日乌鲁木齐开往阿克苏的旅客列车遭遇浮尘天气,由于瞬时大风造成第9至19节车厢脱轨,当时的风力达13级,瞬间最大风速达27.9m/s.根据流体力学知识,流体对物体的作用力可用f=αρ0Av2来表达.其中α为一系数,A为物体的截面积,ρ0为空气密度,v为物体相对于流体的速
今年2月28日乌鲁木齐开往阿克苏的旅客列车遭遇浮尘天气,由于瞬时大风造成第9至19节车厢脱轨,当时的风力达13级,瞬间最大风速达27.9m/s.根据流体力学知识,流体对物体的作用力可用f=αρ0Av2来表达.其中α为一系数,A为物体的截面积,ρ0为空气密度,v为物体相对于流体的速度.已知空气密度ρ0=1.25kg/m3,球体积公式为V=
| 4 |
| 3 |
(1)若有一个特制的风力发电机能在如此恶劣的情况下工作,它将空气的动能转化为电能的效率为20%,有效受风面积为4.0m2,则此发电机在风速为27.9m/s时输出的电功率为多大?(α=0.5)
(2)若某次大风使空气中悬浮微粒浓度达到了5.8×10-6kg/m3,悬浮颗粒的平均密度ρ’为2.0×103kg/m3.悬浮微粒中约
| 1 |
| 50 |
(3)若沙尘颗粒的密度ρs=2.8×103kg/m3,沙尘颗粒为球形,半径r=2.5×10-4m,地球表面处α=0.45,试估算地面附近形成扬沙天气的风速至少为多少?.
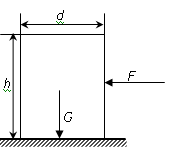
(4)若在大风中有一密度为ρ的立方体恰能被水平方向风力吹得翻倒,推算该物体所受重力与风速的几次方成正比,并请用此结论简要解释火车在大风中脱轨的原因.
分析:(1)空气动能的能的20%转化为电能,根据能量守恒定律列式求解即可;
(2)先求解1m3气体中沙尘的总质量,然后再求解沙尘的总体积,求解出单个平均体积,得到可吸入颗粒;
(3)流体中向各个方向都有压力,当风力f和沙粒的重力满足:f≥mg关系时,方能形成扬沙天气;
(4)当风力的力矩M风等于立方体重力矩MG时,立方体将翻倒,根据力矩平衡条件列式求解即可.
(2)先求解1m3气体中沙尘的总质量,然后再求解沙尘的总体积,求解出单个平均体积,得到可吸入颗粒;
(3)流体中向各个方向都有压力,当风力f和沙粒的重力满足:f≥mg关系时,方能形成扬沙天气;
(4)当风力的力矩M风等于立方体重力矩MG时,立方体将翻倒,根据力矩平衡条件列式求解即可.
解答:解:(1)输出的电功率为:P=f?v?η=αρ0Av2?v?η=αρ0Av3η,式中系数α=0.5
所以 P=0.5×1.25×4×27.93×0.2 W=1.1×104 W
(2)V空=1m3的空气中悬浮微粒的质量为 m=ρ浓V空=5.8×10-8×1kg=5.8×10-8 kg
悬浮微粒的总体积 V=
=
kg=2.9×10-11 m3
单个悬浮微粒的体积
V0=
πr3=
×3.14×(
)3 m3=6.5×10-23 m3
1m3中可吸入颗粒数 n=
=
×2.9×10-11,6.5×10-23)=8.9×1011 个
(3)当风力f 和沙粒的重力满足:f≥mg 关系时,方能形成扬沙天气,即
αρ0Av2=αρ0πr2v2≥ρs×
π r3×g
得 v≥
≈4.07 m/s
(4)设立方体边长为L、重力为G,当风力的力矩M风等于立方体重力矩MG时,立方体将翻倒,所以
f×
=G×
式中 f=αρ0Av2=αρ0L2v2;G=mg=ρVg=ρL3g
得 αρ0L2v2=ρL3g
即 L=
因为 G=ρL3g=ρ×(
)3×g=
v6,可见 G∝v6
所以风速增大时,风力f将急剧增加,从而将火车吹翻,造成脱轨事故.
答:(1)此发电机在风速为27.9m/s时输出的电功率为1.1×104 W;
(2)1.0m3空气中约含有8.9×1011颗可吸入颗粒;
(3)地面附近形成扬沙天气的风速至少为4.07 m/s;
(4)该物体所受重力与风速的六次方成正比,风速增大时,风力f将急剧增加,从而将火车吹翻,造成脱轨事故.
所以 P=0.5×1.25×4×27.93×0.2 W=1.1×104 W
(2)V空=1m3的空气中悬浮微粒的质量为 m=ρ浓V空=5.8×10-8×1kg=5.8×10-8 kg
悬浮微粒的总体积 V=
| m |
| ρ′ |
| 5.8×10-8 |
| 2×103 |
单个悬浮微粒的体积
V0=
| 4 |
| 3 |
| 4 |
| 3 |
| 5×10-8 |
| 2 |
1m3中可吸入颗粒数 n=
| η′V |
| V0 |
| \f(1 |
| 50 |
(3)当风力f 和沙粒的重力满足:f≥mg 关系时,方能形成扬沙天气,即
αρ0Av2=αρ0πr2v2≥ρs×
| 4 |
| 3 |
得 v≥
|
(4)设立方体边长为L、重力为G,当风力的力矩M风等于立方体重力矩MG时,立方体将翻倒,所以
f×
| L |
| 2 |
| L |
| 2 |
式中 f=αρ0Av2=αρ0L2v2;G=mg=ρVg=ρL3g
得 αρ0L2v2=ρL3g
即 L=
| αρ0v2 |
| ρg |
因为 G=ρL3g=ρ×(
| αρ0v2 |
| ρg |
α3
| ||
| ρ2g2 |
所以风速增大时,风力f将急剧增加,从而将火车吹翻,造成脱轨事故.
答:(1)此发电机在风速为27.9m/s时输出的电功率为1.1×104 W;
(2)1.0m3空气中约含有8.9×1011颗可吸入颗粒;
(3)地面附近形成扬沙天气的风速至少为4.07 m/s;
(4)该物体所受重力与风速的六次方成正比,风速增大时,风力f将急剧增加,从而将火车吹翻,造成脱轨事故.
点评:本题四个小问考查的内容各不相同,关键明确流体中向各个方向的压强和压力均相等,同时要能结合能量守恒定律、共点力平衡条件、力矩平衡条件列式求解,较难.

练习册系列答案
相关题目
(13分)风压就是垂直于气流方向上单位面积所受到的风的压力。某工科大学的学生研究小组进行了风洞实验,研究风速和风压之间的关系,得到的实验数据见下表:
风速(m/s) | 2 | 4 | 8 | 12 | 16 | 20 | 24 | 32 |
风压(N/m2) | 2.5 | 10 | 40 | 90 | 160 | 250 | 360 | 640 |
(1)试通过对上述实验数据的分析,归纳出风速v与风压p之间的定量关系;
(2)2007年2月28日凌晨1时55分左右,从乌鲁木齐驶往阿克苏的5806次列车遭遇特大沙尘暴,列车从第1节车厢到第11节车厢相继被吹翻。据铁路部门设在沿线的测风仪纪录,

(3)上述大风能将列车吹翻吗?如果能吹翻,试说明你作出判断的依据是什么?如果不能吹翻,也同样说明理由,并猜测可能是什么因素使列车发生翻转的?在紧急情况下,你能否提出应急措施并作简要说明。
 πr3.
πr3.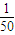 为可吸入颗粒,其平均直径为5×10-8m,求:1.0m3空气中约含有多少颗可吸入颗粒?
为可吸入颗粒,其平均直径为5×10-8m,求:1.0m3空气中约含有多少颗可吸入颗粒?