题目内容
【题目】如图所示，绝缘轨道MNPQ位于同一竖直面内，其中MN段是长度为L的水平轨道，PQ段为足够长的光滑竖直轨道，NP段为光滑的四分之一圆弧，圆心为O，直线NN′右侧有方向水平向左的电场（图中未画出），电场强度E=
，在包含圆弧轨道NP的ONO′P区域内有方向垂直纸面向外、磁感应强度为B的匀强磁场（边界处无磁场）．轨道MN最左端M点处静止一质量为m、电荷量为q的带负电的物块A，一质量为3m为物块C从左侧的光滑轨道上以速度v0撞向物块A．A、C之间只发生一次弹性碰撞，且最终刚好挨在一起停在轨道MN上，A、C均可视为质点，且与轨道MN的动摩擦因数相同，重力加速度为g．A在运动过程中所带电荷量保持不变且始终没有脱离轨道．A第一次到达N点时，对轨道的压力为2mg．求：
（1）碰撞后A、C的速度大小；
（2）A、C与水平轨道MN的动摩擦因数μ；
（3）A对轨道NP的最大压力的大小．
【答案】（1）
；
（2）
（3）
【解析】
（1）A、C发生弹性碰撞，满足动量守恒和动能守恒，列式联立求解碰后A、C的速度；
（2）A在NN′右侧运动过程中，电场力和重力做功之和为0。根据动能定理列式求解A、C与水平轨道MN的动摩擦因数；
（3）将重力和电场力进行等效合成，找到A对轨道NP有最大压力的位置，根据动能定理求解此位置的速度，根据牛顿第二定律求解最大压力.
（1）A、C发生弹性碰撞后的速度分别为vA、vC，则有：
3mv0=mvA+3mvC①
=
+
②
联立①②解得：③
④
（2）设A、C最后静止时与M点的距离为l1，A在NN′右侧运动过程中，电场力和重力做功之和为0。有
μmg（2L－l１）=⑤
μ3mgl１=⑥
联立解得③④⑤⑥μ
⑦
（3）设A在Ｎ点的速度为
，A从M到N的过程中，由动能定理得
⑧
设圆弧NP的半径为a
因为A在Ｎ点时对轨道的压力为2mg，
⑨
A在NN′右侧受到的电场力F=qE=
mg⑩
重力和电场力的合力大小为F合=2mg，方向与OP夹角为
。过O点沿合力方向作直线与圆弧相交于Ｋ点，当A经P点返回N点的过程中到达K点时，达到最大速度
，此时A对轨道的压力最大。
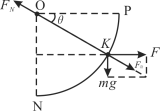
A从M点到K点过程中，由动能定理可得：
返回K点时：FN－F合－
由③⑦⑧⑨⑩得：FN
由牛顿第三定律得A对轨道NP的最大压力为：
