题目内容
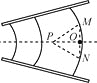
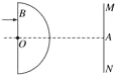
【题目】如图所示,MN为竖直放置的光屏,光屏的左侧有半径为R、折射率为![]() 的透明半球体,O为球心,轴线OA垂直于光屏,O至光屏的距离OA=2
的透明半球体,O为球心,轴线OA垂直于光屏,O至光屏的距离OA=2![]() R.一细束单色光垂直射向半球体的平面,在平面的入射点为B,OB=R,求:
R.一细束单色光垂直射向半球体的平面,在平面的入射点为B,OB=R,求:
(1)光线从透明半球体射出时,出射光线偏离原方向的角度.
(2)光线在光屏形成的光斑到A点的距离.
【答案】(1) 30° (2) R.
【解析】
(1)分析如图.

设入射点B到O的垂直距离BO=h,∠BCO=β,折射角为i.对OBC,由正弦公式得:
sinβ=![]() =
=![]()
又
n=![]() =
=![]()
联立解得
sini=![]()
所以:
i=60°
出射光线偏离原方向的角度:
Δθ=i-β=60°-30°=30°
(2)设出射光线与MN交于P点,与OA交与D点,则由几何关系可得,∠CDQ=30°;所以:
OQ=QD=Rcos 30°=![]() R;
R;
AD=AO-OD=2![]() R-2×
R-2×![]() R=
R=![]() R;
R;
所以:
PA=AD·tan 30°=![]() R×
R×![]() =R.
=R.

 名校课堂系列答案
名校课堂系列答案【题目】某同学设计了一个探究小车的加速度a与小车所受拉力F及质量m关系的实验,图为实验装置简图。所用交变电流的频率为50Hz,小车及车中砝码的质量用m表示,盘及盘中砝码的质量用M表示,小车的加速度可由小车后拖动的纸带上由打点计时器打出的点计算出。
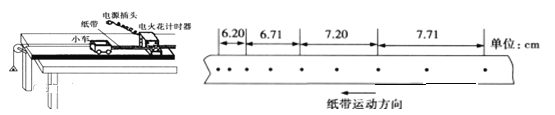
(1)当M与m的大小关系满足_____时,才可以认为绳对小车的拉力大小等于盘和盘中砝码的重力。
(2)某次实验得到的纸带及实验数据如图所示,图中所画点为计数点,相邻计数点之间还有4个点未画出,根据纸带可求出小车的加速度大小为__________![]() 。(保留3位有效数字)
。(保留3位有效数字)
(3)保持盘及盘中砝码的质量不变,改变小车中砝码的质量,分别得到小车加速度a与质量m及对应的![]() ,数据如下表:请在方格坐标纸中画
,数据如下表:请在方格坐标纸中画![]() 图线__________,并从图线求出小车加速度a与质量倒数
图线__________,并从图线求出小车加速度a与质量倒数![]() 之间的关系式是__________。
之间的关系式是__________。
试验次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1.90 | 1.72 | 1.49 | 1.25 | 1.00 | 0.75 | 0.50 | 0.30 |
| 0.25 | 0.29 | 0.33 | 0.40 | 0.50 | 0.71 | 1.00 | 1.67 |
| 4.00 | 3.45 | 3.03 | 2.50 | 2.00 | 1.41 | 1.00 | 0.60 |