题目内容
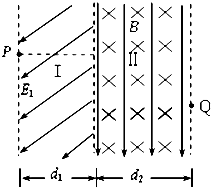
如图所示,K是粒子发生器,D1、D2、D3是三块挡板,通过传感器可控制它们定时开启和关闭,D1、D2的间距为L,D2、D3的间距为
.在以O为原点的直角坐标系Oxy中有一磁感应强度大小为B,方向垂直纸面向里的匀强磁场,y轴和直线MN是它的左、右边界,且MN平行于y轴.现开启挡板D1、D3,粒子发生器仅在t=0时刻沿x轴正方向发射各种速率的粒子,D2仅在t=nT(n=0,1,2…T为已知量)时刻开启,在t=5T时刻,再关闭挡板D3,使粒子无法进入磁场区域.已知挡板的厚度不计,粒子带正电,不计粒子的重力,不计粒子间的相互作用,整个装置都放在真空中.
(1)求能够进入磁场区域的粒子的速度大小;
(2)已知从原点O进入磁场中速度最小的粒子经过坐标为(0,2cm)的P点,应将磁场边界MN在Oxy平面内如何平移,才能使从原点O进入磁场中速度最大的粒子经过坐标为(3
cm,6cm)的Q点?
(3)磁场边界MN平移后,进入磁场中速度最大的粒子经过Q点.如果L=6cm,求速度最大的粒子从D1运动到Q点的时间.

| L |
| 2 |
(1)求能够进入磁场区域的粒子的速度大小;
(2)已知从原点O进入磁场中速度最小的粒子经过坐标为(0,2cm)的P点,应将磁场边界MN在Oxy平面内如何平移,才能使从原点O进入磁场中速度最大的粒子经过坐标为(3
| 3 |
(3)磁场边界MN平移后,进入磁场中速度最大的粒子经过Q点.如果L=6cm,求速度最大的粒子从D1运动到Q点的时间.

(1)设能够进入磁场区域的粒子的速度大小为vm,由题意,粒子由D1到D2经历的时间为:△t1=mT=
(m=1、2…)
粒子由D2到D3经历的时间为:△t2=
=
t=5T时刻,挡板D3关闭,粒子无法进入磁场,故有:
△t=△t1+△t2≤5T
联立以上三式解得:m=1、2、3
所以,能够进入磁场区域的粒子的速度为:
vm=
(m=1、2、3)
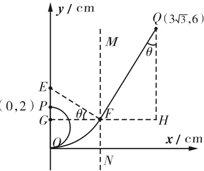
(2)进入磁场中速度最小的粒子经过坐标为(0cm,2cm)的P点,所以R=1cm.粒子在磁场中匀速圆周运动,洛伦兹力提供向心力为:qvB=m
所以,粒子圆周运动的半径为:R=
由前可知,进入磁场中粒子的最大速度是最小速度的3倍,故:R′=3R=3cm
由图知:3cosθ+FH=3
FH=(6-3+3sinθ)tanθ
解得:θ=300 FH=
cm
因此,只要将磁场区域的边界MN平行左移
cm到F点,速度最大的粒子在F点穿出磁场,将沿圆轨迹的切线方向到达Q点.
(3)粒子在K到O之间运动时:v=
得:t1=
T
粒子 磁场中的运动:t2=
=
粒子从F到Q点做匀速直线运动,时间:t3=
=
T
解得:t=t1+t2+t3=(
+
+
)T
答:(1)能够进入磁场区域的粒子的速度大小为vm=
(m=1、2、3);
(2)只要将磁场区域的边界MN平行左移
cm到F点,速度最大的粒子在F点穿出磁场,将沿圆轨迹的切线方向到达Q点;
(3)磁场边界MN平移后,进入磁场中速度最大的粒子经过Q点.如果L=6cm,求速度最大的粒子从D1运动到Q点的时间为(
+
+
)T
| L |
| vm |
粒子由D2到D3经历的时间为:△t2=
| L |
| 2vm |
| mT |
| 2 |
t=5T时刻,挡板D3关闭,粒子无法进入磁场,故有:
△t=△t1+△t2≤5T
联立以上三式解得:m=1、2、3
所以,能够进入磁场区域的粒子的速度为:
vm=
| L |
| mT |
(2)进入磁场中速度最小的粒子经过坐标为(0cm,2cm)的P点,所以R=1cm.粒子在磁场中匀速圆周运动,洛伦兹力提供向心力为:qvB=m
| v2 |
| R |
所以,粒子圆周运动的半径为:R=
| mv |
| Bq |
由前可知,进入磁场中粒子的最大速度是最小速度的3倍,故:R′=3R=3cm
由图知:3cosθ+FH=3
| 3 |
FH=(6-3+3sinθ)tanθ
解得:θ=300 FH=
3
| ||
| 2 |
因此,只要将磁场区域的边界MN平行左移
3
| ||
| 2 |
(3)粒子在K到O之间运动时:v=
| L |
| T |
| 3 |
| 2 |
粒子 磁场中的运动:t2=
| πR |
| 3v |
| πT |
| 6 |
粒子从F到Q点做匀速直线运动,时间:t3=
| FH |
| sinθ?v |
| ||
| 2 |
解得:t=t1+t2+t3=(
| 3 |
| 2 |
| π |
| 6 |
| ||
| 2 |
答:(1)能够进入磁场区域的粒子的速度大小为vm=
| L |
| mT |
(2)只要将磁场区域的边界MN平行左移
3
| ||
| 2 |
(3)磁场边界MN平移后,进入磁场中速度最大的粒子经过Q点.如果L=6cm,求速度最大的粒子从D1运动到Q点的时间为(
| 3 |
| 2 |
| π |
| 6 |
| ||
| 2 |


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目