题目内容
12.一个人在地球上所受重力为882N,在月球上所受重力约为147N,月球和地球半径之比约为$\frac{1}{4}$,地球上的第一宇宙速度为7.9km/s,则月球上的第一宇宙速度约为多少?分析 在靠近星体表面飞行时重力等于向心力,得到近地卫星的速度表达式,再根据重力加速度g和半径关系求出月球的近月卫星运行速率
解答 解:在靠近星体表面飞行时重力等于向心力:
mg=m$\frac{{v}^{2}}{R}$
故第一宇宙速度V=$\sqrt{gR}$.
一个人在地球上所受重力为882N,在月球上所受重力约为147N,则重力加速度之比为g地:g月=882:147=6:1
所以第一宇宙速度比为v地:v月=$\frac{\sqrt{{g}_{地}{R}_{地}}}{\sqrt{{g}_{月}{R}_{月}}}$=$\sqrt{\frac{4}{1}×\frac{6}{1}}$=$\frac{\sqrt{24}}{1}$
故月球的第一宇宙速度为v=$\frac{1}{\sqrt{24}}×7.9$km/s=1.61km/s
答:月球上的第一宇宙速度约为1.61km/s
点评 万有引力提供圆周运动向心力是解题的入手,熟练掌握相关公式及其变形是正确解题的关键,在靠近星体表面飞行时重力等于向心力.

练习册系列答案
相关题目
7. 一列简谐波在某时刻的波形图如图所示,质点M在该时刻的振动速度为v,经过0.2s,M点振动速度仍为v,再经过0.2s,M的速度变为-v,则该波( )
一列简谐波在某时刻的波形图如图所示,质点M在该时刻的振动速度为v,经过0.2s,M点振动速度仍为v,再经过0.2s,M的速度变为-v,则该波( )
 一列简谐波在某时刻的波形图如图所示,质点M在该时刻的振动速度为v,经过0.2s,M点振动速度仍为v,再经过0.2s,M的速度变为-v,则该波( )
一列简谐波在某时刻的波形图如图所示,质点M在该时刻的振动速度为v,经过0.2s,M点振动速度仍为v,再经过0.2s,M的速度变为-v,则该波( )| A. | 向左传播,波速为10m/s | B. | 向左传播,波速为5m/s | ||
| C. | 向右传播,波速为10m/s | D. | 向右传播,波速为5m/s |
1.某空间中出现了如图中虚线所示的一组闭合的电场线,这可能是( )


| A. | 在中心点O有一静止的点电荷 | B. | 沿AB方向有通有恒定电流的直导线 | ||
| C. | 沿BA方向的磁场在减弱 | D. | 沿AB方向的磁场在减弱 |
2. 如图所示,理想变压器原线圈匝数n1=1 210,副线圈匝数n2=121,原线圈电压u=220$\sqrt{2}$sin 100πt V,负载电阻R=44Ω,不计电表对电路的影响,各电表的读数应为( )
如图所示,理想变压器原线圈匝数n1=1 210,副线圈匝数n2=121,原线圈电压u=220$\sqrt{2}$sin 100πt V,负载电阻R=44Ω,不计电表对电路的影响,各电表的读数应为( )
 如图所示,理想变压器原线圈匝数n1=1 210,副线圈匝数n2=121,原线圈电压u=220$\sqrt{2}$sin 100πt V,负载电阻R=44Ω,不计电表对电路的影响,各电表的读数应为( )
如图所示,理想变压器原线圈匝数n1=1 210,副线圈匝数n2=121,原线圈电压u=220$\sqrt{2}$sin 100πt V,负载电阻R=44Ω,不计电表对电路的影响,各电表的读数应为( )| A. | A1读数为0.5 A | B. | V1读数为311 V | C. | A2读数为0.5 A | D. | V2读数为31.1 V |
 如图所示,为楼层间运送物体的传送装置,浅色传送带的水平部分ab=3.2m,斜面部分bc=7.5625m,bc与水平面的夹角θ=37°.一煤块A与传送带的动摩擦因数始终为μ=0.25,传送带沿图示的方向运动,速率v=5m/s.若把煤块A轻放到a处,它将被传送带送到c点,且煤块A不会脱离传送带,煤块A相对传送带滑动时会在传送带上留下黑色痕迹.求煤块A从a点被传送到c点在传送带上留下黑色痕迹的长度.(已知:sin 37°=0.6,cos 37°=0.8,g=10m/s2)
如图所示,为楼层间运送物体的传送装置,浅色传送带的水平部分ab=3.2m,斜面部分bc=7.5625m,bc与水平面的夹角θ=37°.一煤块A与传送带的动摩擦因数始终为μ=0.25,传送带沿图示的方向运动,速率v=5m/s.若把煤块A轻放到a处,它将被传送带送到c点,且煤块A不会脱离传送带,煤块A相对传送带滑动时会在传送带上留下黑色痕迹.求煤块A从a点被传送到c点在传送带上留下黑色痕迹的长度.(已知:sin 37°=0.6,cos 37°=0.8,g=10m/s2)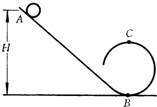 如图所示,斜槽轨道下端与一个半径为0.4m的圆形轨道相连接.一个质量为0.1kg的物体从高为H=2m的A点由静止开始滑下,运动到圆形轨道的最高点C处时,对轨道的压力等于物体的重力.求物体从A运动到C的过程中克服摩擦力所做的功(g取10m/s2).
如图所示,斜槽轨道下端与一个半径为0.4m的圆形轨道相连接.一个质量为0.1kg的物体从高为H=2m的A点由静止开始滑下,运动到圆形轨道的最高点C处时,对轨道的压力等于物体的重力.求物体从A运动到C的过程中克服摩擦力所做的功(g取10m/s2). 正弦交变电流的电压最大值为220$\sqrt{2}$v,负载电阻R=440Ω,若不考虑电表内阻对电路的影响,则交流电压表的读数为220VV,交流电流表的读数为0.5V.
正弦交变电流的电压最大值为220$\sqrt{2}$v,负载电阻R=440Ω,若不考虑电表内阻对电路的影响,则交流电压表的读数为220VV,交流电流表的读数为0.5V. 如图所示,气缸开口向上放置在水平平台上,活塞质量为10kg,横截面积50cm2,厚度不计,气缸全长20cm,大气压强为1×105Pa,活塞封闭的气柱长10cm,若将气缸倒过来放置时,活塞下方的空气能通过平台上的缺口与大气相通.g取10m/s2,求气柱多长?
如图所示,气缸开口向上放置在水平平台上,活塞质量为10kg,横截面积50cm2,厚度不计,气缸全长20cm,大气压强为1×105Pa,活塞封闭的气柱长10cm,若将气缸倒过来放置时,活塞下方的空气能通过平台上的缺口与大气相通.g取10m/s2,求气柱多长?