题目内容
10.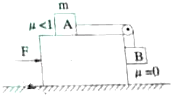 如图所示,质量为M的滑块C放在光滑的桌面上,质量均为m两物体A和B用细绳连接,A平放在滑块上,与滑块间动摩擦因数为μ,细绳跨过滑轮后将B物体竖直悬挂,设绳和轮质量不计,轮轴不受摩擦力作用,水平推力F作用于滑块,为使A和B滑块保持相对静止,F至少应为多大?
如图所示,质量为M的滑块C放在光滑的桌面上,质量均为m两物体A和B用细绳连接,A平放在滑块上,与滑块间动摩擦因数为μ,细绳跨过滑轮后将B物体竖直悬挂,设绳和轮质量不计,轮轴不受摩擦力作用,水平推力F作用于滑块,为使A和B滑块保持相对静止,F至少应为多大?
分析 隔离对B分析,抓住B竖直方向上合力为零,求出绳子的拉力,隔离对A分析,结合牛顿第二定律求出加速度,再对整体分析,结合牛顿第二定律求出F的最小值.
解答 解:隔离对B分析,因为B竖直方向保持静止,则竖直方向上合力为零,有T=mg,
隔离对A分析,
①当A相对C向前运动,根据牛顿第二定律得,a=$\frac{T-μmg}{m}=\frac{mg-μmg}{m}=(1-μ)g$,
对A、B、C整体分析,
F=(M+2m)a,
解得F=(M+2m)(1-μ)g.
②当A相对C向后运动,根据牛顿第二定律得,a=$\frac{T+μmg}{m}=\frac{mg+μmg}{m}=(1+μ)g$,
对A、B、C整体分析,
F=(M+2m)a,
解得F=(M+2m)(1+μ)g.
答:F的大小为(M+2m)(1-μ)g<F<(M+2m)(1+μ)g.
点评 本题考查了牛顿第二定律的临界问题,关键抓住临界状态,采用整体法和隔离法进行求解,难度中等.

练习册系列答案
相关题目
1.某科技小组制作的利用太阳能驱动小车,当太阳光照射到小车上的光电板时,光电板中产生的电能经电动机带动小车前进.若小车在平直的公路上以初速度v0开始加速行驶,经过时间t,前进了距离l,达到最大速度vmax,设此过程中电动机功率恒为额定功率P,受的阻力恒为Ff,小车的质量为m.则此过程中电动机所做的功为( )
| A. | Ffvmaxt | B. | Pt | ||
| C. | Ff$\frac{{v}_{0}+{v}_{max}}{2}$t | D. | $\frac{1}{2}$mvmax2+Ffl-$\frac{1}{2}$mv02 |
18.下列设想中,符合能量转化和守恒定律的是( )
| A. | 利用永久磁铁和软铁的相互作用,制成一台机器,不消耗能量而不停地转动 | |
| B. | 制造一架飞机,不携带燃料,只需利用太阳能飞行 | |
| C. | 做成一只船,利用风的能量行驶,不用其他动力 | |
| D. | 利用核动力,驾驶地球离开太阳系 |
6.将一磁铁缓慢或者迅速地由闭合线圈外的某一位置插到线圈中的同一位置处,不会发生变化的物理量是( )
| A. | 磁通量的变化量 | B. | 磁通量的变化率 | ||
| C. | 感应电流的大小 | D. | 流过导体横截面的电荷量 |
3. 如图所示的水平传送带静止时,一个小物块A以某一水平初速度从传送带左端冲上传送带,然后从传送带右端以一个较小的速度V滑出传送带;若传送带在皮带轮带动下以大于V的速度运动时,A物块仍以相同的水平速度冲上传送带,且传送带的速度小于A的初速度,则( )
如图所示的水平传送带静止时,一个小物块A以某一水平初速度从传送带左端冲上传送带,然后从传送带右端以一个较小的速度V滑出传送带;若传送带在皮带轮带动下以大于V的速度运动时,A物块仍以相同的水平速度冲上传送带,且传送带的速度小于A的初速度,则( )
 如图所示的水平传送带静止时,一个小物块A以某一水平初速度从传送带左端冲上传送带,然后从传送带右端以一个较小的速度V滑出传送带;若传送带在皮带轮带动下以大于V的速度运动时,A物块仍以相同的水平速度冲上传送带,且传送带的速度小于A的初速度,则( )
如图所示的水平传送带静止时,一个小物块A以某一水平初速度从传送带左端冲上传送带,然后从传送带右端以一个较小的速度V滑出传送带;若传送带在皮带轮带动下以大于V的速度运动时,A物块仍以相同的水平速度冲上传送带,且传送带的速度小于A的初速度,则( )| A. | 若皮带轮逆时针转动,A物块仍以速度V离开传送带 | |
| B. | 若皮带轮逆时针方向转动,A物块不可能到达传送带的右端 | |
| C. | 若皮带轮顺时针方向转动,A物块离开传送带的速度仍然可能为V | |
| D. | 若皮带轮顺时针方向转动,A物块离开传送带右端的速度一定大于V |
4.下列关于矢量和标量的说法中,正确的是( )
| A. | 矢量既有大小又有方向,标量只有大小没有方向 | |
| B. | 既有大小又有方向的物理量一定是矢量 | |
| C. | 矢量运算时和标量一样,直接将其大小相加或相减即可 | |
| D. | 矢量和标量的根本区别在于运算法则不同 |
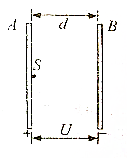 如图所示,A,B两块相距d平行放置的圆形金属板,A板带正电,B板带负电,两板间电压为U.在A板中心处放有一放射源S,S可向各个方向均匀发出质量为m,电量为+q,初速率为v0的带电粒子.要使从S射出的带电粒子全部打在B板上,求B板面积应至少多大?
如图所示,A,B两块相距d平行放置的圆形金属板,A板带正电,B板带负电,两板间电压为U.在A板中心处放有一放射源S,S可向各个方向均匀发出质量为m,电量为+q,初速率为v0的带电粒子.要使从S射出的带电粒子全部打在B板上,求B板面积应至少多大?