题目内容
6. 在发射地球同步卫星的过程中,卫星首先进入椭圆轨道Ⅰ,然后在Q点通过改变卫星速度,让卫星进入地球同步轨道Ⅱ.则( )
在发射地球同步卫星的过程中,卫星首先进入椭圆轨道Ⅰ,然后在Q点通过改变卫星速度,让卫星进入地球同步轨道Ⅱ.则( )| A. | 该卫星变轨前后的速度相等 | |
| B. | 在轨道Ⅰ上,卫星在P点的速度大于在Q点的速度 | |
| C. | 卫星在同步轨道Ⅱ上的运行速度大于7.9km/s | |
| D. | 卫星在Q点通过加速实现由轨道Ⅰ进入轨道Ⅱ |
分析 根据万有引力提供向心力,得出线速度与轨道半径的关系,从而比较出卫星在同步轨道上的速度与第一宇宙速度的大小.根据万有引力做功情况判断卫星在P点和Q点的动能大小.根据开普勒第三定律比较在轨道上的运行周期.
解答 解:A、卫星在Q点的万有引力提供加速度,在轨道Ⅱ上经过Q点的万有引力等于向心力,而在轨道Ⅰ上经过Q点时万有引力等于需要的向心力,根据需要的向心力的公式:F=m$\frac{{v}^{2}}{r}$,可知在轨道Ⅱ上经过Q点的速度大于在轨道Ⅰ上经过Q点的速度.故A错误;
B、在轨道Ⅰ上,由P点向Q点运动,万有引力做负功,动能减小,所以P点的速度大于Q点的速度.故B正确.
C、根据$\frac{GMm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$,知v=$\sqrt{\frac{GM}{r}}$,第一宇宙速度的轨道半径等于地球的半径,知7.9km/s是卫星绕地球做圆周运动的最大环绕速度,所以卫星在同步轨道Ⅱ上的运行速度小于7.9 km/s.故C错误.
D、卫星在Q点通过加速实现由轨道Ⅰ进入轨道Ⅱ,故D正确;
故选:BD.
点评 解决本题的关键掌握万有引力提供向心力以及开普勒第三定律,并能灵活运用.

练习册系列答案
相关题目
16. 如图所示,一细束a光和一细束b光平行射到同一个三棱镜上,经折射后交于光屏上的同一个点M,若用n1和n2分别表示三棱镜对a光和b光的折射率,用v1和v2分别表示a光和b光在三棱镜中的光速,用λ1和λ2分别表示a光和b光在三棱镜中的波长,下列说法正确的是( )
如图所示,一细束a光和一细束b光平行射到同一个三棱镜上,经折射后交于光屏上的同一个点M,若用n1和n2分别表示三棱镜对a光和b光的折射率,用v1和v2分别表示a光和b光在三棱镜中的光速,用λ1和λ2分别表示a光和b光在三棱镜中的波长,下列说法正确的是( )
 如图所示,一细束a光和一细束b光平行射到同一个三棱镜上,经折射后交于光屏上的同一个点M,若用n1和n2分别表示三棱镜对a光和b光的折射率,用v1和v2分别表示a光和b光在三棱镜中的光速,用λ1和λ2分别表示a光和b光在三棱镜中的波长,下列说法正确的是( )
如图所示,一细束a光和一细束b光平行射到同一个三棱镜上,经折射后交于光屏上的同一个点M,若用n1和n2分别表示三棱镜对a光和b光的折射率,用v1和v2分别表示a光和b光在三棱镜中的光速,用λ1和λ2分别表示a光和b光在三棱镜中的波长,下列说法正确的是( )| A. | n1>n2,λ1<λ2,v1<v2 | B. | n1<n2,λ1<λ2,v1<v2 | ||
| C. | n1<n2,λ1>λ2,v1<v2 | D. | n1>n2,λ1<λ2,v1>v2 |
17.人造卫星绕地球作匀速圆周运动,关于它运转的轨道平面,下列情况不可能的有( )
| A. | 运转轨道平面与赤道平面是重合的 | |
| B. | 轨道平面与某经线所在平面是重合的 | |
| C. | 轨道平面与赤道以外的某纬线所在平面是重合的 | |
| D. | 轨道平面通过地球球心,但平面与任一纬线和经线均不重合 |
1. 如图所示,一导线弯成半径为a的半圆形闭合回路.虚线MN右侧有磁感应强度为B的匀强磁场,方向垂直于回路所在的平面.回路以速度v向右匀速进入磁场,直径CD始终与MN垂直.从D点到达边界开始到C点进入磁场为止,下列结论正确的是( )
如图所示,一导线弯成半径为a的半圆形闭合回路.虚线MN右侧有磁感应强度为B的匀强磁场,方向垂直于回路所在的平面.回路以速度v向右匀速进入磁场,直径CD始终与MN垂直.从D点到达边界开始到C点进入磁场为止,下列结论正确的是( )
 如图所示,一导线弯成半径为a的半圆形闭合回路.虚线MN右侧有磁感应强度为B的匀强磁场,方向垂直于回路所在的平面.回路以速度v向右匀速进入磁场,直径CD始终与MN垂直.从D点到达边界开始到C点进入磁场为止,下列结论正确的是( )
如图所示,一导线弯成半径为a的半圆形闭合回路.虚线MN右侧有磁感应强度为B的匀强磁场,方向垂直于回路所在的平面.回路以速度v向右匀速进入磁场,直径CD始终与MN垂直.从D点到达边界开始到C点进入磁场为止,下列结论正确的是( )| A. | 感应电流方向改变 | B. | CD段直线始终不受安培力 | ||
| C. | 感应电动势最大值E=Bav | D. | 感应电动势平均值E=$\frac{1}{4}$πBav |
18.如图所示的变压器电路中有五个相同的定值电阻,理想变压器原,副线圈的匝数比为1:2,现在a,b端输入正弦交流电,则R1和R2的功率之比为( )
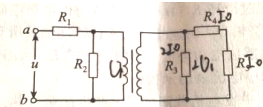

| A. | 49:1 | B. | 24:1 | C. | 7:1 | D. | 3:1 |
15. 如图所示,将一束由两种色光混合的复色光沿SE方向射向一上、下表面平行的厚玻璃平面镜上表面,得到三束光线A、B、C,若平面镜的上、下表面足够宽,则( )
如图所示,将一束由两种色光混合的复色光沿SE方向射向一上、下表面平行的厚玻璃平面镜上表面,得到三束光线A、B、C,若平面镜的上、下表面足够宽,则( )
 如图所示,将一束由两种色光混合的复色光沿SE方向射向一上、下表面平行的厚玻璃平面镜上表面,得到三束光线A、B、C,若平面镜的上、下表面足够宽,则( )
如图所示,将一束由两种色光混合的复色光沿SE方向射向一上、下表面平行的厚玻璃平面镜上表面,得到三束光线A、B、C,若平面镜的上、下表面足够宽,则( )| A. | 光束A为单色光,光束B、C为复色光 | |
| B. | 玻璃对光束C的折射率大于对光束B的折射率 | |
| C. | A、B、C三束光线一定互相平行 | |
| D. | 通过相同的双缝干涉装置,光束B产生的相邻条纹间距要大于光束C产生的相邻亮条纹间距 |
 金属棒bc在两光滑的水平固定放置的平行金属导轨上向右运动,回路中有垂直纸面向里的匀强磁场,这时回路中感应电流的方向为逆时针(填“顺时针”或“逆时针”),bc棒将受到方向向左(填“左”或“右”)的安培力;为使bc棒向右匀速运动,必须对bc棒施加方向向右(填“左”或“右”)的外力.
金属棒bc在两光滑的水平固定放置的平行金属导轨上向右运动,回路中有垂直纸面向里的匀强磁场,这时回路中感应电流的方向为逆时针(填“顺时针”或“逆时针”),bc棒将受到方向向左(填“左”或“右”)的安培力;为使bc棒向右匀速运动,必须对bc棒施加方向向右(填“左”或“右”)的外力. 如图所示的装置也可完成《验证动量守恒》的实验,某同学把两块大小不同的木块用细线连接,中间夹一被压缩了的轻质弹簧,将这一系统置于光滑的水平桌面上,烧断细线,观察木块的运动情况,进行必要的测量,验证物体间相互作用时动量守恒.
如图所示的装置也可完成《验证动量守恒》的实验,某同学把两块大小不同的木块用细线连接,中间夹一被压缩了的轻质弹簧,将这一系统置于光滑的水平桌面上,烧断细线,观察木块的运动情况,进行必要的测量,验证物体间相互作用时动量守恒.