题目内容
4.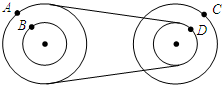 两个大轮半径相等的皮带轮的结构如图所示,AB两点的半径之比为2:1,CD两点的半径之比也为2:1,则ABCD四点的角速度之比为1:1:2:2,这四点的线速度之比为2:1:4:2,向心加速度之比为2:1:8:4.
两个大轮半径相等的皮带轮的结构如图所示,AB两点的半径之比为2:1,CD两点的半径之比也为2:1,则ABCD四点的角速度之比为1:1:2:2,这四点的线速度之比为2:1:4:2,向心加速度之比为2:1:8:4.
分析 皮带不打滑,A和D两点线速度大小相等,由公式v=ωr,角速度与半径成反比,求出角速度之比,A、B;C、D在同一轮上,角速度相同,进而求出四点线速度、角速度的比例关系,由公式an=$\frac{{v}^{2}}{r}$研究向心加速度关系.
解答 解:皮带不打滑,A和D两点线速度大小相等,由公式v=ωr,得到:ωA:ωD:=rD:rA=1:2.
A、B;C、D在同一轮上,角速度相同,
所以ωA:ωB:ωC:ωD=1:1:2:2
所以线速度之比为:vA:vB:vC:vD=2:1:4:2
根据an=$\frac{{v}^{2}}{r}$得:向心加速度之比为aA:aB:aC:aD=2:1:8:4
故答案为:1:1:2:2;2:1:4:2;2:1:8:4.
点评 本题是圆周运动中典型问题,关键抓住相等量:皮带不打滑时,两轮边缘上各点的线速度大小相等;同一轮上各点的角速度相同.

练习册系列答案
相关题目
14.如图所示是一定质量的气体从状态A经B到状态C再到状态A的p-T图象,由图可知( )
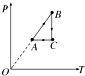

| A. | VA=VB | B. | VB>VC | C. | VB=VC | D. | VA>VC |
15. 如图,放于竖直面内的光滑金属圆环半径为R=0.4m,质量为m的带孔小球穿于环上,同时有一长也为R的细绳一端系于球上,另一端系于圆环最低点.当圆环以角速度ω绕竖直直径转动时,绳被拉直且小球受二个力作用.(g=10m/s2 )则ω为( )
如图,放于竖直面内的光滑金属圆环半径为R=0.4m,质量为m的带孔小球穿于环上,同时有一长也为R的细绳一端系于球上,另一端系于圆环最低点.当圆环以角速度ω绕竖直直径转动时,绳被拉直且小球受二个力作用.(g=10m/s2 )则ω为( )
 如图,放于竖直面内的光滑金属圆环半径为R=0.4m,质量为m的带孔小球穿于环上,同时有一长也为R的细绳一端系于球上,另一端系于圆环最低点.当圆环以角速度ω绕竖直直径转动时,绳被拉直且小球受二个力作用.(g=10m/s2 )则ω为( )
如图,放于竖直面内的光滑金属圆环半径为R=0.4m,质量为m的带孔小球穿于环上,同时有一长也为R的细绳一端系于球上,另一端系于圆环最低点.当圆环以角速度ω绕竖直直径转动时,绳被拉直且小球受二个力作用.(g=10m/s2 )则ω为( )| A. | 5$\sqrt{3}$rad/s | B. | 7.5rad/s | C. | 5$\sqrt{2}$rad/s | D. | 5rad/s |
19.为了估算一个天体的质量,需要知道绕该天体做匀速圆周运动的另一星球的条件是( )(引力常量G为已知):
①运转周期和轨道半径 ②质量和运转周期 ③轨道半径和加速度 ④环绕速度和质量.
①运转周期和轨道半径 ②质量和运转周期 ③轨道半径和加速度 ④环绕速度和质量.
| A. | ①或③ | B. | ①或④ | C. | ②或③ | D. | ②或④ |
16.下列关于物体做斜抛运动的叙述,正确的是( )
| A. | 物体受到变力作用,且力的方向与初速度不在一条直线 | |
| B. | 物体受到恒力作用,且力的方向与初速度垂直时,物体做斜抛运动 | |
| C. | 物体受到恒力作用,且力的方向与初速度不在一条直线上,物体一定做斜抛运动 | |
| D. | 物体只受重力作用,且力的方向与初速度不在一条直线 上,也不垂直时,物体一定做斜抛运动 |
13.关于弹性势能,下列说法正确的是( )
| A. | 弹性势能与物体的形变量有关 | |
| B. | 弹性势能与物体的形变量无关 | |
| C. | 物体运动的速度越大,弹性势能越大 | |
| D. | 弹性势能与物体的速度无关 |
20.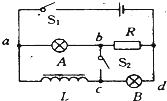 如图所示,电灯A和B与固定电阻的阻值均为R,L是自感系数较大的线圈,当S1闭合、S2断开且电路稳定时A、B亮度相同;再闭合S2,待电路稳定后将S1断开;下列说法中正确的是( )
如图所示,电灯A和B与固定电阻的阻值均为R,L是自感系数较大的线圈,当S1闭合、S2断开且电路稳定时A、B亮度相同;再闭合S2,待电路稳定后将S1断开;下列说法中正确的是( )
 如图所示,电灯A和B与固定电阻的阻值均为R,L是自感系数较大的线圈,当S1闭合、S2断开且电路稳定时A、B亮度相同;再闭合S2,待电路稳定后将S1断开;下列说法中正确的是( )
如图所示,电灯A和B与固定电阻的阻值均为R,L是自感系数较大的线圈,当S1闭合、S2断开且电路稳定时A、B亮度相同;再闭合S2,待电路稳定后将S1断开;下列说法中正确的是( )| A. | A灯立即熄灭 | B. | A灯将比原来更亮一些后再熄灭 | ||
| C. | 有电流通过B灯,方向为c→d | D. | 有电流通过A灯,方向为b→a |
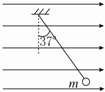 一根长为L的丝线一端固定在天花板上,另一端吊着一质量为m、带电荷量为q的小球静止在水平向右的匀强电场中,如图所示,丝线与竖直方向成37°角.天花板距离地面高度为2L.(重力加速度为g,sin37°=0.6),求:
一根长为L的丝线一端固定在天花板上,另一端吊着一质量为m、带电荷量为q的小球静止在水平向右的匀强电场中,如图所示,丝线与竖直方向成37°角.天花板距离地面高度为2L.(重力加速度为g,sin37°=0.6),求: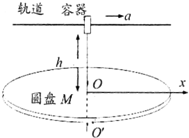 如图所示,M是水平放置的半径足够大的圆盘,绕过其圆心的竖直轴OO′匀速转动,规定经过圆心O点且水平向右为x轴正方向.在O点正上方距盘面高为h=5m处有一个可间断滴水的容器,从t=0时刻开始,容器沿水平轨道向x轴正方向做初速度为零的匀加速直线运动.已知t=0时刻滴下第一滴水,以后每当前一滴水刚好落到盘面时再滴下一滴水.则:(取g=10m/s2)
如图所示,M是水平放置的半径足够大的圆盘,绕过其圆心的竖直轴OO′匀速转动,规定经过圆心O点且水平向右为x轴正方向.在O点正上方距盘面高为h=5m处有一个可间断滴水的容器,从t=0时刻开始,容器沿水平轨道向x轴正方向做初速度为零的匀加速直线运动.已知t=0时刻滴下第一滴水,以后每当前一滴水刚好落到盘面时再滴下一滴水.则:(取g=10m/s2)