题目内容
14.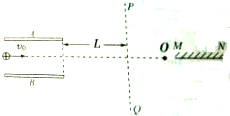 空间有两个长为l间距为d的平行金属板AB水平放置,在两板间施加电压UAB,如图,平行板的右侧有一竖直的虚线PQ,且平行板右侧与PQ间无场区,PQ右侧的O点有一固定的点电荷和一接收屏MN,且O点和接收屏MN均在平行板的中轴线上,现有一质量为m,带电量为q的粒子,从平行板左侧中央位置以v0的速度进入平行板,最终带电粒子以与离开平行板等大的速率垂直MN被接收.已知l=8cm,d=8cm,UAB=300V,q=10-10C,m=10-20kg,L=12cm,v0=2×106m/s,静电力常量为k=9×109N•m2/C2,忽略粒子的重力,求:
空间有两个长为l间距为d的平行金属板AB水平放置,在两板间施加电压UAB,如图,平行板的右侧有一竖直的虚线PQ,且平行板右侧与PQ间无场区,PQ右侧的O点有一固定的点电荷和一接收屏MN,且O点和接收屏MN均在平行板的中轴线上,现有一质量为m,带电量为q的粒子,从平行板左侧中央位置以v0的速度进入平行板,最终带电粒子以与离开平行板等大的速率垂直MN被接收.已知l=8cm,d=8cm,UAB=300V,q=10-10C,m=10-20kg,L=12cm,v0=2×106m/s,静电力常量为k=9×109N•m2/C2,忽略粒子的重力,求:(1)粒子到达虚线PQ时,距离中轴线的间距多大?
(2)点O到PQ的间距和固定在O点电荷的电量.
分析 (1)粒子在平行板中做类平抛运动,根据运动学公式求得离开平行板的速度和偏转量,根据几何关系求得到中轴线的距离;
(2)粒子以与离开平行板等大的速率垂直MN被接收,故粒子乙点电荷为圆心,由几何关系求的距离,库仑力提供向心力即可求得电荷
解答 解:(1)粒子在平行板间的加速度为$a=\frac{q{U}_{AB}}{md}=\frac{1{0}^{-10}×300}{1{0}^{-20}×0.08}m/{s}^{2}=3.75×1{0}^{13}m/{s}^{2}$
通过平行板的时间为t=$\frac{l}{{v}_{0}}=\frac{0.08}{2×1{0}^{6}}s=4×1{0}^{-8}s$
${v}_{y}=at=1.5×1{0}^{6}m/s$
离开平行板的速度为v=$\sqrt{{v}_{0}^{2}{+v}_{y}^{2}}=2.5×1{0}^{6}m/s$
与水平方向的夹角为$tanθ=\frac{{v}_{y}}{{v}_{0}}=\frac{3}{4}$
粒子在平行板中的偏转量为$y=\frac{1}{2}a{t}^{2}=\frac{1}{2}×3.75×1{0}^{13}×(4×1{0}^{-8})^{2}$m=0.03m
由几何关系可知$\frac{\frac{l}{2}+L}{\frac{l}{2}}=\frac{Y}{y}$
解得Y=0.12m
(2)带电粒子以与离开平行板等大的速率垂直MN被接收,故粒子静茹点电荷区域后粒子力点电荷为圆心做匀速圆周运动,
如图: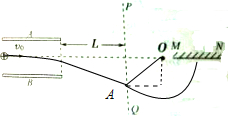
有几何关系可知$d′=Ytanθ=0.03×\frac{3}{4}m=0.0225m$
r=$\sqrt{{Y}^{2}+d{′}^{2}}=\sqrt{0.0{3}^{2}+0.022{5}^{2}}m=0.075m$
$k\frac{Qq}{{r}^{2}}=\frac{m{v}^{2}}{r}$
解得Q=5.2×10-9C
答:(1)粒子到达虚线PQ时,距离中轴线的间距为0.03m
(2)点O到PQ的间距为0.0225m固定在O点电荷的电量5.2×10-9C.
点评 本题主要考查了粒子在平行板中做类平抛运动,根据运动学公式求的,抓住粒子以点电荷为圆心做匀速圆周运动,库仑力提供向心力即可

 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案 如图所示为一个小灯泡的电流与它两端电压的变化关系曲线.若把三个这样的灯泡串联后,接到电压恒定的12V电源上,则此时流过小灯泡的电流和小灯泡的电阻分别为( )
如图所示为一个小灯泡的电流与它两端电压的变化关系曲线.若把三个这样的灯泡串联后,接到电压恒定的12V电源上,则此时流过小灯泡的电流和小灯泡的电阻分别为( )| A. | I=0.4 A;R=10Ω | B. | I=0.2A;R=60Ω | C. | I=0.4 A;R=30Ω | D. | I=0.6A;R=20Ω |
| A. | 物体受到离心力的作用,将做离心运动 | |
| B. | 做匀速圆周运动的物体,在外界提供的向心力突然变大时,将做近心运动 | |
| C. | 做匀速圆周运动的物体,在外界提供的向心力突然变小或消失时,将做离心运动 | |
| D. | 物体做离心运动的根本原因是惯性 |
| A. | F=0 | B. | $F=m\frac{R_0^2a}{{{{({R_0}+h)}^2}}}$ | ||
| C. | $F=m\root{3}{{a{r^2}ω_0^4}}$ | D. | $F=m\frac{r^2}{{{R_0}+h}}a$ |

| A. | 5s-15s内做匀加速运动,加速度为0.8m/s2 | |
| B. | 前5s内静止 | |
| C. | 15s-20s内做匀减速运动,加速度为-0.8m/s2 | |
| D. | 质点15s末离出发点最远,20秒末回到出发点 |
 如图所示,质量均为1kg的滑块A和木板B最初静止在带有挡板的粗糙斜面的底端,斜面倾角为θ=37°,现用大小为14N的力F沿斜面向上拉木板B,在力F作用的同时,给滑块A一个沿斜面向上的初速度v0=6m/s,若A与B间的滑动摩擦系数为μ1=$\frac{1}{4}$,木板B与斜面间的摩擦系数为μ2=$\frac{1}{2}$,最大静摩擦力等于滑动摩擦力,取g=10m/s2,斜面和木板足够长,(sin37°=0.6,cos37°=0.8)求:
如图所示,质量均为1kg的滑块A和木板B最初静止在带有挡板的粗糙斜面的底端,斜面倾角为θ=37°,现用大小为14N的力F沿斜面向上拉木板B,在力F作用的同时,给滑块A一个沿斜面向上的初速度v0=6m/s,若A与B间的滑动摩擦系数为μ1=$\frac{1}{4}$,木板B与斜面间的摩擦系数为μ2=$\frac{1}{2}$,最大静摩擦力等于滑动摩擦力,取g=10m/s2,斜面和木板足够长,(sin37°=0.6,cos37°=0.8)求:




 如图所示,M、N为加速电场的两极板,M板中心有一小孔Q,其正上方有一半径为R1=1m的圆形磁场区域,圆心为0,另有一内半径为R1,外半径为R2=$\sqrt{3}$m的同心环形磁场区域,区域边界与M板相切于Q点,磁感应强度大小均为B=0.5T,方向相反,均垂直于纸面.一比荷$\frac{q}{m}$=4×107C/kg带正电粒子从靠近N板的P点由静止释放,经加速后通过小孔Q,垂直进入环形磁场区域.已知点P、Q、O在同一竖直线上,不计粒子的重力,且不考虑粒子的相对论效应.
如图所示,M、N为加速电场的两极板,M板中心有一小孔Q,其正上方有一半径为R1=1m的圆形磁场区域,圆心为0,另有一内半径为R1,外半径为R2=$\sqrt{3}$m的同心环形磁场区域,区域边界与M板相切于Q点,磁感应强度大小均为B=0.5T,方向相反,均垂直于纸面.一比荷$\frac{q}{m}$=4×107C/kg带正电粒子从靠近N板的P点由静止释放,经加速后通过小孔Q,垂直进入环形磁场区域.已知点P、Q、O在同一竖直线上,不计粒子的重力,且不考虑粒子的相对论效应.