题目内容
2.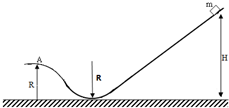 如图,两个光滑圆形轨道平滑连接后与光滑斜轨道平滑连接,圆形轨道半径均为R,质量为m的物块从高H处由静止开始滑下,
如图,两个光滑圆形轨道平滑连接后与光滑斜轨道平滑连接,圆形轨道半径均为R,质量为m的物块从高H处由静止开始滑下,(1)物块滑到B点时对轨道压力是多少?
(2)要使物块能滑过A点(即在A点时的速度大于零)又不失去抓地力 (即物体对地面压力N>0)物块离地面高度h的取值范围是多少?
分析 (1)物块在光滑轨道下滑的过程,遵守机械能守恒,由机械能守恒定律求出物块滑到B点时的速度.在B点,由重力和轨道的支持力的合力提供物体所需要的向心力,根据牛顿运动定律求解物块滑到B点时对轨道压力.
(2)根据机械能守恒求出物块能滑过A点时h的值.再根据抓地力N>0,求出h的值,即可得到所求的范围.
解答 解:(1)轨道都是光滑的,由机械能守恒有:$mgH=\frac{1}{2}mv_B^2$
物块在B 点时做圆周运动:$N-mg=m\frac{v_B^2}{R}$
得 $N=(\frac{2H}{R}+1)mg$
由牛顿第二定律得,物块对轨道压力大小 N′=N=$(\frac{2H}{R}+1)$mg
(2)轨道都是光滑的,由机械能守恒有:$mgH=\frac{1}{2}mv_A^2+mgR$---------①
小车在A点时,由圆周运动规律得:$mg-N=m\frac{v_A^2}{R}$----------②
要使物体能滑过A点,vA>0
由①可得:h>R
要使小车不失去抓地力,即N>0
由①②解得 $h<\frac{3}{2}R$
所以 $R<h<\frac{3}{2}R$
答:
(1)物块滑到B点时对轨道压力是$(\frac{2H}{R}+1)$mg.
(2)物块离地面高度h的取值范围是 $R<h<\frac{3}{2}R$.
点评 解决本题的关键要明确圆周运动向心力的来源,把握最高点A的临界条件,由机械能守恒定律和牛顿运动定律结合处理此类问题.

练习册系列答案
相关题目
13.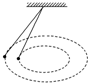 长度不同的两根细绳,悬挂于同一点,另一端各系一个质量相同的小球,使它们在同一水平面内做圆锥摆运动,如图所示,则( )
长度不同的两根细绳,悬挂于同一点,另一端各系一个质量相同的小球,使它们在同一水平面内做圆锥摆运动,如图所示,则( )
 长度不同的两根细绳,悬挂于同一点,另一端各系一个质量相同的小球,使它们在同一水平面内做圆锥摆运动,如图所示,则( )
长度不同的两根细绳,悬挂于同一点,另一端各系一个质量相同的小球,使它们在同一水平面内做圆锥摆运动,如图所示,则( )| A. | 它们的周期相同 | B. | 较长的绳所系小球的周期较大 | ||
| C. | 两球的向心力与半径成正比 | D. | 两绳张力与绳长成正比 |
10.如图所示,当小车向右加速运动时,物块M相对车厢静止于竖直车厢壁上,当车的加速度增大时( ) 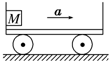

| A. | M受静摩擦力增大 | B. | M对车厢壁的压力减小 | ||
| C. | M仍相对于车厢静止 | D. | M受静摩擦力减小 |
12. 质量为M的球用长为L的悬线固定于O点,在O点正下方$\frac{L}{2}$处有一颗钉子,把悬线拉直与竖直方向成一定角度,由静止释放小球,如图所示,当悬线碰到钉子时,下列说法正确的是( )
质量为M的球用长为L的悬线固定于O点,在O点正下方$\frac{L}{2}$处有一颗钉子,把悬线拉直与竖直方向成一定角度,由静止释放小球,如图所示,当悬线碰到钉子时,下列说法正确的是( )
 质量为M的球用长为L的悬线固定于O点,在O点正下方$\frac{L}{2}$处有一颗钉子,把悬线拉直与竖直方向成一定角度,由静止释放小球,如图所示,当悬线碰到钉子时,下列说法正确的是( )
质量为M的球用长为L的悬线固定于O点,在O点正下方$\frac{L}{2}$处有一颗钉子,把悬线拉直与竖直方向成一定角度,由静止释放小球,如图所示,当悬线碰到钉子时,下列说法正确的是( )| A. | 小球的机械能突然减少 | B. | 小球的向心加速度突然增大 | ||
| C. | 小球的角速度突然减小 | D. | 悬线的张力突然增大 |
 有一质量m=1kg小环套在长L=0.5m的固定的轻杆的上端,轻杆与水平方向成θ=37°.由静止释放小球,经过t=0.5s小球到达轻杆底端.(sin37°=0.6,cos37°=0.8,g=10m/s2)试求:
有一质量m=1kg小环套在长L=0.5m的固定的轻杆的上端,轻杆与水平方向成θ=37°.由静止释放小球,经过t=0.5s小球到达轻杆底端.(sin37°=0.6,cos37°=0.8,g=10m/s2)试求: