题目内容
一质量为m，带电量为q的带电粒子以初速度v0，从上板边沿水平向右射入两板间的电场中．已知平行板长为l，两板的距离为d，电势差为U，粒子重力不计．求：①带电粒子运动的加速度a；
②粒子射出电场时的速度偏转角正切值．
分析：（1）粒子在电场中受到电场力作用，电场力使粒子产生加速度a；
（2）类子在电场中做类平抛运动，根据类平抛运动规律求解粒子射出电场时的速度偏转角正切值．
（2）类子在电场中做类平抛运动，根据类平抛运动规律求解粒子射出电场时的速度偏转角正切值．
解答：解：（1）粒子在电场中受到电场力大小为F=qE，
两平行板间电场为匀强电场，根据电场强度和电势差的关系有：
E=
所以粒子受电场力为F=qE=
根据牛顿第二定律粒子产生的加速度a=
=
（2）粒子在电场中做类平抛运动，初速度v0，加速度a=
粒子在水平方向做匀速直线运动，所以粒子射出电场在水平方向产生位移x=l
所以粒子在电场中运动时间t=
粒子在竖直方向的速度vy=at=
如图粒子射出电场时速度偏转角的正切值tanθ=
=
答：①带电粒子运动的加速度a=
；
②粒子射出电场时的速度偏转角正切值为
．
两平行板间电场为匀强电场，根据电场强度和电势差的关系有：
E=
| U |
| d |
所以粒子受电场力为F=qE=
| qU |
| d |
根据牛顿第二定律粒子产生的加速度a=
| F |
| m |
| qU |
| md |
（2）粒子在电场中做类平抛运动，初速度v0，加速度a=
| qU |
| md |
粒子在水平方向做匀速直线运动，所以粒子射出电场在水平方向产生位移x=l
所以粒子在电场中运动时间t=
| l |
| v0 |
粒子在竖直方向的速度vy=at=
| qUl |
| mdv0 |
如图粒子射出电场时速度偏转角的正切值tanθ=
| vy |
| v0 |
| qUl | ||
md
|
答：①带电粒子运动的加速度a=
| qU |
| md |
②粒子射出电场时的速度偏转角正切值为
| qUl | ||
md
|
点评：带电粒子在电场中的运动，若垂直电场线进入则做类平抛运动，要将运动分解为沿电场线和垂直于电场线两个方向进行分析，利用直线运动的规律进行求解．
练习册系列答案
相关题目
真空中存在竖直向上的匀强电场和水平方向的匀强磁场，一质量为m，带电量为q的物体以速度v在竖直平面内做半径为R的匀速圆周运动，假设t=0时刻物体在轨迹最低点且重力势能为零，电势能也为零，那么，下列说法正确的是（ ）
如图所示，在直角坐标系的第一象限中存在沿y轴负方向的匀强电场，电场强度大小为E，在第四象限中存在着垂直纸面的匀强磁场，一质量为m、带电量为q的粒子（不计重力）在y轴上的A点以平行x轴的初速度v0射人电场区，然后从电场区进入磁场区，又从磁场区进入电场区，并通过x轴上P点和Q点各一次，已知P点坐标为（a，0），Q点坐标为（b，0），求磁感应强度的大小和方向？
如图所示，L为竖直、固定的光滑绝缘杆，杆上o点套有一质量为m、带电量为-q的小环，在杆的左侧固定一电荷量为+Q的点电荷，杆上a、b两点到+Q的距离相等，oa之间距离为h1，ab之间距离为h2，使小环从图示位置的o点由静止释放后，通过a点的速率为| 3gh1 |
| A、小环通过a、b两点时的速度大小相等 | ||
B、小环通过b点的速率为
| ||
| C、小环在oa之间的速度不断增大 | ||
| D、小环从o到b，电场力做的功可能为零 |
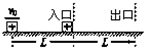如图所示，在宽度为L的两虚线区域内存在匀强电场，一质量为m，带电量为+q的滑块（可看成点电荷），从距该区域为L的绝缘水平面上以初速度v0向右运动并进入电场区域，滑块与水平面间的动摩擦因数为μ．
如图所示，直角坐标平面xOy内有一条直线AC过坐标原点O与x轴成45°夹角，在OA与x轴负半轴之间的区域内存在垂直xOy平面向外的匀强磁场B，在OC与x轴正半轴之间的区域内存在垂直xOy平面向外的匀强磁场B2．现有一质量为m，带电量为q（q＞0）的带电粒子以速度v从位于直线AC上的P点，坐标为（L，L），竖直向下射出，经测量发现，此带电粒子每经过相同的时间T，会再将回到P点，已知距感应强度