题目内容
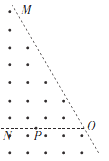
【题目】如图所示,OM的左侧存在范围足够大、磁感应强度大小为B的匀强磁场,磁场方向垂直纸面向外,ON(在纸面内)与磁场方向垂直且∠NOM=60°,ON上有一点P,OP=L。P点有一个粒子源,可沿纸面内各个方向射出质量为m、电荷量为q的带正电粒子(重力不计),速率均为![]() ,则粒子在磁场中运动的最短时间为
,则粒子在磁场中运动的最短时间为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
由题设条件求出粒子做匀速圆周运动的半径r,结合左手定则粒子做逆时针方向匀速圆周运动,粒子运动时间t最短时,所转过的圆心角θ最小,所对的弦也最短,画出最短的弦,再作出粒子在磁场中做匀速圆周运动最短时间的轨迹,由几何关系求出此种情况下粒子的偏转角θ,从而求出了最短时间.
粒子进入磁场中做匀速圆周运动则有:![]() ,而将题设的v值代入得:
,而将题设的v值代入得:![]() ,分析可知:粒子运动的时间t最短时,所粒子偏转的角度θ最小,则θ所对弦最短,作PB⊥OM于B点,PB即为最短的弦,结合左手定则,以
,分析可知:粒子运动的时间t最短时,所粒子偏转的角度θ最小,则θ所对弦最短,作PB⊥OM于B点,PB即为最短的弦,结合左手定则,以![]() 为半径作出过P、B两点的轨迹圆如图所示,O′为圆心;
为半径作出过P、B两点的轨迹圆如图所示,O′为圆心;

根据几何关系有:O′B=O′P=![]() …①;PB=Lsin60°=
…①;PB=Lsin60°=![]() L…②;联立①②式可得:PB=
L…②;联立①②式可得:PB=![]() O′B,则粒子偏转的角度:θ=90°;结合周期公式:
O′B,则粒子偏转的角度:θ=90°;结合周期公式:![]() ,可知粒子在磁场中运动的最短时间为:
,可知粒子在磁场中运动的最短时间为:![]() ,故A正确,BCD错误。故选A。
,故A正确,BCD错误。故选A。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目