题目内容
 质量为m=2kg 的物体在光滑的水平面上运动,在水平面上建立x0y坐标系,t=0时,物体位于坐标系的原点0.物体在x轴和y轴方向上的分速度vx、vy随时间t变化的图象如图甲、乙所示.求:
质量为m=2kg 的物体在光滑的水平面上运动,在水平面上建立x0y坐标系,t=0时,物体位于坐标系的原点0.物体在x轴和y轴方向上的分速度vx、vy随时间t变化的图象如图甲、乙所示.求:(1)t=3.0s时,物体受到的合力的大小和方向;
(2)t=8.0s时,物体速度的大小和方向;
(3)t=8.0s时,物体的位置(用位置坐标x、y表示)
分析:(1)由速度图象求出物体的加速度,由牛顿第二定律求出物体受到的合力;
(2)由速度图象求出物体在8s时沿x轴与y轴的速度,由平行四边形定则求出物体的速度;
(3)由匀速直线运动的位移公式求出物体在x轴上的位移;
由匀变速直线运动的位移公式求出在y轴上的位移,然后确定物体的坐标位置.
(2)由速度图象求出物体在8s时沿x轴与y轴的速度,由平行四边形定则求出物体的速度;
(3)由匀速直线运动的位移公式求出物体在x轴上的位移;
由匀变速直线运动的位移公式求出在y轴上的位移,然后确定物体的坐标位置.
解答:解:(1)由图甲所示图象可知,物体在x轴上做匀速直线运动,所受合力:Fx=0N,
物体在y轴方向上做匀加速直线运动,加速度:ay=
=
=0.5m/s2,
由牛顿第二定律得:Fy=may=2×0.5=1N,则物体受到的合力大小是1N,沿y轴正方向;
(2)由图象可得,在t=8s时,vx=3m/s,vy=4m/s,
则物体的速度:v=
=
=5m/s,
设速度方向与x轴间的夹角为θ,则:tanθ=
=
,
则θ=arctan
;
(3)t=8.0s时,物体的在x轴方向的位移:x=vxt=3×8=24(m),
在y轴方向的位移:y=
ayt2=
×0.5×82=16m,
则物体的位置坐标是(24m,16m);
故答案为:(1)大小:1N,方向:沿y轴正方向;
(2)大小:5m/s,方向:与x轴夹角θ=arctan
;
(3)(24m,16m).
物体在y轴方向上做匀加速直线运动,加速度:ay=
| △v |
| △t |
| 4-0 |
| 8-0 |
由牛顿第二定律得:Fy=may=2×0.5=1N,则物体受到的合力大小是1N,沿y轴正方向;
(2)由图象可得,在t=8s时,vx=3m/s,vy=4m/s,
则物体的速度:v=
|
| 32+42 |
设速度方向与x轴间的夹角为θ,则:tanθ=
| vy |
| vx |
| 4 |
| 3 |
则θ=arctan
| 4 |
| 3 |
(3)t=8.0s时,物体的在x轴方向的位移:x=vxt=3×8=24(m),
在y轴方向的位移:y=
| 1 |
| 2 |
| 1 |
| 2 |
则物体的位置坐标是(24m,16m);
故答案为:(1)大小:1N,方向:沿y轴正方向;
(2)大小:5m/s,方向:与x轴夹角θ=arctan
| 4 |
| 3 |
(3)(24m,16m).
点评:由v-t图象求出速度与加速度是正确解题的前提与关键,熟练应用牛顿第二定律、位移公式即可正确解题.

练习册系列答案
相关题目
 质量为m=2kg的物体,放在水平面上,它们之间的动摩擦因数μ=0.5,现对物体施F=20N的水平作用力,如图所示,物体运动4s后撤去力F到物体再停止时,通过的总路程是多少?
质量为m=2kg的物体,放在水平面上,它们之间的动摩擦因数μ=0.5,现对物体施F=20N的水平作用力,如图所示,物体运动4s后撤去力F到物体再停止时,通过的总路程是多少?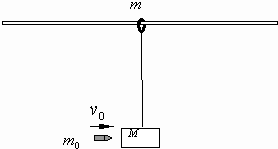 在足够长的光滑固定水平杆上,套有一个质量为m=0.5kg的光滑圆环.一根长为L=lm的轻绳,一端拴在环上,另一端系着一个质量为M=2kg的木块,如图所示.现有一质量为m0=20g的子弹以v0=1000m/s的水平速度射入木块,子弹穿出木块时的速度为u=200m/s,子弹与木块作用的时间极短,取g=10m/s2.求:当子弹射穿木块后,木块向右摆动的最大高度h.
在足够长的光滑固定水平杆上,套有一个质量为m=0.5kg的光滑圆环.一根长为L=lm的轻绳,一端拴在环上,另一端系着一个质量为M=2kg的木块,如图所示.现有一质量为m0=20g的子弹以v0=1000m/s的水平速度射入木块,子弹穿出木块时的速度为u=200m/s,子弹与木块作用的时间极短,取g=10m/s2.求:当子弹射穿木块后,木块向右摆动的最大高度h.