题目内容
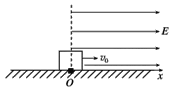
【题目】在一个水平面上建立x轴，在过原点O垂直于x轴的平面的右侧空间有一个匀强电场，场强大小E=6.0×105 N/C，方向与x轴正方向相同，在原点O处放一个质量m=0.01 kg带负电荷的绝缘物块，其带电荷量q= -5×10－8 C．物块与水平面间的动摩擦因数μ=0.2，给物块一个沿x轴正方向的初速度v0=2 m/s.如图所示．试求：
(1)物块沿x轴正方向运动的加速度；
(2)物块沿x轴正方向运动的最远距离；
(3)物体运动的总时间为多长？
【答案】(1)5 m/s2 (2)0.4 m (3)1.74 s
【解析】带负电的物块以初速度v0沿x轴正方向进入电场中，受到向左的电场力和滑动摩擦力作用，做匀减速运动，当速度为零时运动到最远处，根据动能定理列式求解；分三段进行研究：在电场中物块向右匀减速运动，向左匀加速运动，离开电场后匀减速运动．根据运动学公式和牛顿第二定律结合列式，求出各段时间，即可得到总时间。
（1）由牛顿第二定律可得
，得
（2）物块进入电场向右运动的过程，根据动能定理得：
。
代入数据，得：s1=0.4m
（3）物块先向右作匀减速直线运动，根据：
，得：t1=0.4s
接着物块向左作匀加速直线运动：
。
根据：
得
物块离开电场后，向左作匀减速运动：
根据：
解得
物块运动的总时间为：
练习册系列答案
相关题目
