题目内容
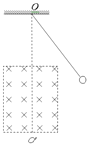
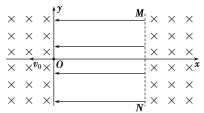
【题目】如图所示，真空中的矩形abcd区域内存在竖直向下的匀强电场，半径为R的圆形区域内同时存在垂直于纸面向里的匀强磁场，磁感应强度为B，圆形边界分别相切于ad、bc边的中点e、f.一带电粒子以初速度v0沿着ef方向射入该区域后能做直线运动；当撤去磁场并保留电场，粒子以相同的初速度沿着ef方向射入恰能从c点飞离该区域.已知ad＝bc＝
R，忽略粒子的重力.求：
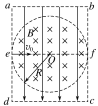
(1)带电粒子的比荷；
(2)若撤去电场保留磁场，粒子离开矩形区域时的位置.
【答案】(1) 
(2)粒子从ab边射出，距b点
【解析】(1)设匀强电场强度为E，当电场和磁场同时存在时，粒子沿ef方向做直线运动，
有qv0B＝qE
当撤去磁场，保留电场时，带电粒子做类平抛运动，水平方向做匀速直线运动，竖直方向做初速度为零的匀加速直线运动，由题知，粒子恰能从c点飞出，则
2R＝v0t，
R＝
at2，qE＝ma
联解得：
＝
(2)
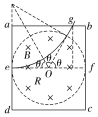
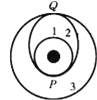
若撤去电场保留磁场，粒子将在洛伦兹力作用下做匀速圆周运动，轨迹如图所示.设粒子离开矩形区域时的位置g离b的距离为x，则由牛顿第二定律；qv0B＝
得r＝R，由图中几何关系θ＝60°
故粒子离开矩形区域时到b的距离为x＝R－R×
＝
故粒子将从ab边射出，距b点.
练习册系列答案
相关题目
