题目内容
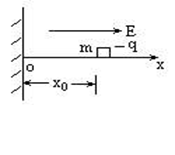
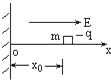 如图,一个质量m,带电荷-q的小物块,可在水平绝缘轨道ox上运动,O端有一与轨道垂直的绝缘固定墙,轨道处于匀强电场中,场强大小为E=
如图,一个质量m,带电荷-q的小物块,可在水平绝缘轨道ox上运动,O端有一与轨道垂直的绝缘固定墙,轨道处于匀强电场中,场强大小为E=| 3μmg | 2q |
(1)小物块到达离墙最远处所用的时间;
(2)小物块第一次到达墙时的速度;
(3)设小物块与墙壁碰撞时不损失机械能,且电量保持不变,则它在停止运动前所通过的总路程多大?
分析:(1)物块向右做匀减速直线运动,由牛顿第二定律求出加速度,然后由速度公式求出运动时间.
(2)求出到达墙壁最远处的位移,然后由动能定理求出第一次到达墙壁时的速度.
(3)物块在运动过程中克服摩擦力做功,使它的机械能减少,最终物块要静止在墙壁处,由动能定理可以求出物块总路程.
(2)求出到达墙壁最远处的位移,然后由动能定理求出第一次到达墙壁时的速度.
(3)物块在运动过程中克服摩擦力做功,使它的机械能减少,最终物块要静止在墙壁处,由动能定理可以求出物块总路程.
解答:解:(1)由牛顿第二定律得:qE+μmg=ma ①
由匀变速运动的速度公式得:v0=at,②
已知电场强度:E=
③
由①②③解得:t=
④
(2)从位置x0处到最远处的位移:x=
t=
v0t ⑤
返回过程,由动能定理得:(qE-μmg)(x0+x)=
mv2-0,⑥
由③④⑤⑥解得:v=
⑦;
(3)因电场力大于摩擦力,故小物块最终停在墙壁处,
全程由动能定理得:qEx0-μmgs=0-
mv2 ⑧
由③⑧解得:s=
x0+
⑨;
答:(1)小物块到达离墙最远处所用的时间为
;
(2)小物块第一次到达墙时的速度为
;
(3)物块在停止运动前所通过的总路程为
x0+
.
由匀变速运动的速度公式得:v0=at,②
已知电场强度:E=
| 3μmg |
| 2q |
由①②③解得:t=
| 2v0 |
| 5μg |
(2)从位置x0处到最远处的位移:x=
. |
| v |
| 1 |
| 2 |
返回过程,由动能定理得:(qE-μmg)(x0+x)=
| 1 |
| 2 |
由③④⑤⑥解得:v=
μgx0+
|
(3)因电场力大于摩擦力,故小物块最终停在墙壁处,
全程由动能定理得:qEx0-μmgs=0-
| 1 |
| 2 |
由③⑧解得:s=
| 3 |
| 2 |
| ||
| 2μg |
答:(1)小物块到达离墙最远处所用的时间为
| 2v0 |
| 5μg |
(2)小物块第一次到达墙时的速度为
μgx0+
|
(3)物块在停止运动前所通过的总路程为
| 3 |
| 2 |
| ||
| 2μg |
点评:分析清楚物体运动过程是正确解题的关键,应用牛顿第二定律、运动学公式与动能定理即可正确解题.

练习册系列答案
相关题目
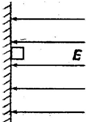 如图所示,一个质量m,带正电q的物体处于场强按E=E0__kt(E0、k均为大于零的常数,取水平向左为正方向)变化的电场中,物体与竖直墙壁间的动摩擦因数为μ,当t=0时,物体处于静止状态.若电场空间和墙面均足够大,下列说法正确的是( )
如图所示,一个质量m,带正电q的物体处于场强按E=E0__kt(E0、k均为大于零的常数,取水平向左为正方向)变化的电场中,物体与竖直墙壁间的动摩擦因数为μ,当t=0时,物体处于静止状态.若电场空间和墙面均足够大,下列说法正确的是( )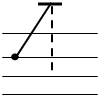 一个质量m=30g带电量为q=1.0×10-8C的半径极小的小球,用丝线悬挂在某匀强电场中,电场线水平.当小球静止时,测得悬线与竖直方向成45°.如图所示.此场强方向如何?场强大小是多少?
一个质量m=30g带电量为q=1.0×10-8C的半径极小的小球,用丝线悬挂在某匀强电场中,电场线水平.当小球静止时,测得悬线与竖直方向成45°.如图所示.此场强方向如何?场强大小是多少?